题目内容
已知A、B、C是直线l上不同的三点,O是l外一点,向量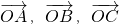 满足:
满足: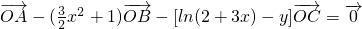 .记y=f(x).
.记y=f(x).
(Ⅰ)求函数y=f(x)的解析式:
(Ⅱ)若对任意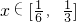 ,不等式|a-lnx|-ln[f'(x)-3x]>0恒成立,求实数a的取值范围:
,不等式|a-lnx|-ln[f'(x)-3x]>0恒成立,求实数a的取值范围:
(Ⅲ)若关于x的方程f(x)=2x+b在(0,1]上恰有两个不同的实根,求实数b的取值范围.
解:(Ⅰ)向量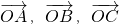 满足:
满足: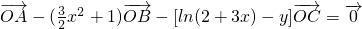 .
.
∴
∵A、B、C是直线l上不同的三点
∴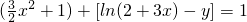
∴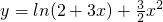
∴f(x)= ;
;
(Ⅱ)∵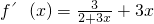 ,∴原不等式为
,∴原不等式为 .
.
得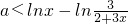 ,或
,或 ,①…(4分)
,①…(4分)
设 ,
,
依题意知a<g(x)或a>h(x)在x∈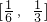 上恒成立,
上恒成立,
∵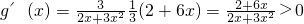 ,
,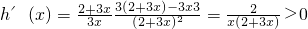 ,
,
∴g(x)与h(x)在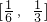 上都是增函数,要使不等式①成立,
上都是增函数,要使不等式①成立,
当且仅当 或
或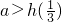 ,∴
,∴ ,或
,或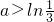 .…(8分)
.…(8分)
(Ⅲ)方程f(x)=2x+b即为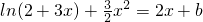 ,
,
变形为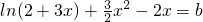 .
.
令φ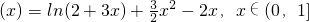 ,
,
∴φ …(10分)
…(10分)
列表写出x,φ'(x),φ(x)在[0,1]上的变化情况:
…(12分)
显然φ(x)在(0,1]上的极小值也即为它的最小值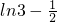 .
.
现在比较ln2与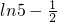 的大小;
的大小;
∵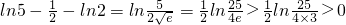 ,∴
,∴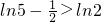 .
.
∴要使原方程在(0,1]上恰有两个不同的实根,必须使 .
.
即实数b的取值范围为 .…(14分)
.…(14分)
分析:(Ⅰ)根据向量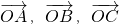 满足:
满足: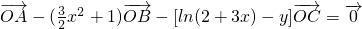 ,结合A、B、C是直线l上不同的三点,即可求函数y=f(x)的解析式;
,结合A、B、C是直线l上不同的三点,即可求函数y=f(x)的解析式;
(Ⅱ)求导函数,原不等式为 ,得
,得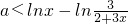 ,或
,或 ,分别求出对应函数的最小值与最大值,即可求得结论;
,分别求出对应函数的最小值与最大值,即可求得结论;
(Ⅲ)方程f(x)=2x+b变形为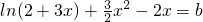 ,研究左边对应函数的最值,即可求得实数b的取值范围.
,研究左边对应函数的最值,即可求得实数b的取值范围.
点评:本题考查导数知识的运用,考查向量知识,考查函数的单调性与最值,考查函数与方程思想,属于中档题.
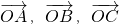 满足:
满足: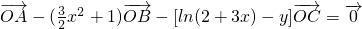 .
.∴

∵A、B、C是直线l上不同的三点
∴
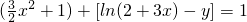
∴
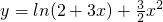
∴f(x)=
 ;
;(Ⅱ)∵
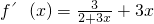 ,∴原不等式为
,∴原不等式为 .
.得
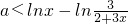 ,或
,或 ,①…(4分)
,①…(4分)设
 ,
,依题意知a<g(x)或a>h(x)在x∈
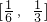 上恒成立,
上恒成立,∵
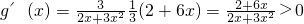 ,
,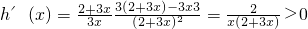 ,
,∴g(x)与h(x)在
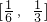 上都是增函数,要使不等式①成立,
上都是增函数,要使不等式①成立,当且仅当
 或
或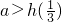 ,∴
,∴ ,或
,或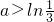 .…(8分)
.…(8分)(Ⅲ)方程f(x)=2x+b即为
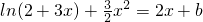 ,
,变形为
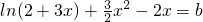 .
.令φ
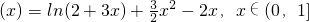 ,
,∴φ
 …(10分)
…(10分)列表写出x,φ'(x),φ(x)在[0,1]上的变化情况:
| x | 0 | (0, ) ) |  | ( ,1) ,1) | 1 |
| ?φ'(x) | 小于0 | 0 | 大于0 | ||
| ?φ(x) | ln2 | 单调递减 | 取极小值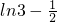 | 单调递增 | 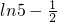 |
显然φ(x)在(0,1]上的极小值也即为它的最小值
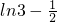 .
.现在比较ln2与
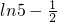 的大小;
的大小;∵
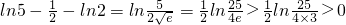 ,∴
,∴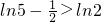 .
.∴要使原方程在(0,1]上恰有两个不同的实根,必须使
 .
.即实数b的取值范围为
 .…(14分)
.…(14分)分析:(Ⅰ)根据向量
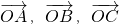 满足:
满足: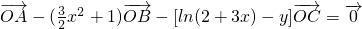 ,结合A、B、C是直线l上不同的三点,即可求函数y=f(x)的解析式;
,结合A、B、C是直线l上不同的三点,即可求函数y=f(x)的解析式;(Ⅱ)求导函数,原不等式为
 ,得
,得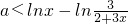 ,或
,或 ,分别求出对应函数的最小值与最大值,即可求得结论;
,分别求出对应函数的最小值与最大值,即可求得结论;(Ⅲ)方程f(x)=2x+b变形为
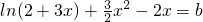 ,研究左边对应函数的最值,即可求得实数b的取值范围.
,研究左边对应函数的最值,即可求得实数b的取值范围.点评:本题考查导数知识的运用,考查向量知识,考查函数的单调性与最值,考查函数与方程思想,属于中档题.

练习册系列答案
相关题目