题目内容
设函数f(x)=x2+bln(x+1),其中b≠0.(Ⅰ)当
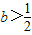 时,判断函数f(x)在定义域上的单调性;
时,判断函数f(x)在定义域上的单调性;(Ⅱ)求函数f(x)的极值点;
(Ⅲ)证明对任意的正整数n,不等式
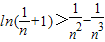 都成立.
都成立.
【答案】分析:(Ⅰ)先求函数的定义域,然后求出函数f(x)的导函数,利用二次函数的性质判定导函数的符号,从而确定函数f(x)在定义域上的单调性;
(Ⅱ)需要分类讨论,由(Ⅰ)可知分类标准为b≥ ,0<b<
,0<b< ,b≤0或f'(x)<0.参数取某些特定值时,可只管作出判断,单列为一类;不能作出直观判断的,再分为一类,用通法解决,另外要注意由f'(x)=0求得的根不一定就是极值点,需要判断在该点两侧的异号性后才能称为“极值点”.
,b≤0或f'(x)<0.参数取某些特定值时,可只管作出判断,单列为一类;不能作出直观判断的,再分为一类,用通法解决,另外要注意由f'(x)=0求得的根不一定就是极值点,需要判断在该点两侧的异号性后才能称为“极值点”.
(Ⅲ)先构造函数h(x)=x3-x2+ln(x+1),然后研究h(x)在[0,+∞)上的单调性,求出函数h(x)的最小值,从而得到ln(x+1)>x2-x3,最后令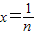 ,即可证得结论.
,即可证得结论.
解答:解:(Ⅰ)函数f(x)=x2+bln(x+1)的定义域在(-1,+∞)
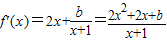
令g(x)=2x2+2x+b,则g(x)在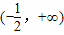 上递增,在
上递增,在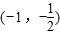 上递减,
上递减,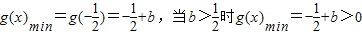
g(x)=2x2+2x+b>0在(-1,+∞)上恒成立,
所以f'(x)>0即当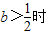 ,函数f(x)在定义域(-1,+∞)上单调递增.
,函数f(x)在定义域(-1,+∞)上单调递增.
(Ⅱ)(1)由(Ⅰ)知当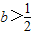 时函数f(x)无极值点
时函数f(x)无极值点
(2)当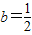 时,
时,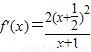 ,
,
∴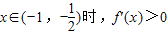
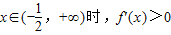 ,
,
∴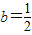 时,函数f(x)在(-1,+∞)上无极值点
时,函数f(x)在(-1,+∞)上无极值点
(3)当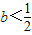 时,解f'(x)=0得两个不同解
时,解f'(x)=0得两个不同解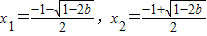
当b<0时,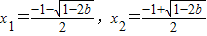 ,
,
∴x1∈(-∞,-1),x2∈(-1,+∞),此时f(x)在(-1,+∞)上有唯一的极小值点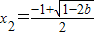
当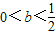 时,x1,x2∈(-1,+∞)f'(x)在(-1,x1),(x2,+∞)都大于0,
时,x1,x2∈(-1,+∞)f'(x)在(-1,x1),(x2,+∞)都大于0,
f'(x)在(x1,x2)上小于0,此时f(x)有一个极大值点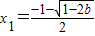 和一个极小值点
和一个极小值点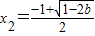
综上可知,b<0,时,f(x)在(-1,+∞)上有唯一的极小值点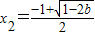
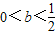 时,f(x)有一个极大值点
时,f(x)有一个极大值点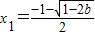 和一个极小值点
和一个极小值点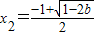
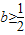 时,函数f(x)在(-1,+∞)上无极值点.
时,函数f(x)在(-1,+∞)上无极值点.
(Ⅲ)当b=-1时,f(x)=x2-ln(x+1).令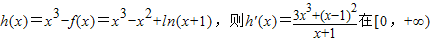 上恒正
上恒正
∴h(x)在[0,+∞)上单调递增,
当x∈(0,+∞)时,恒有h(x)>h(0)=0
即当x∈(0,+∞)时,有x3-x2+ln(x+1)>0,ln(x+1)>x2-x3,对任意正整数n,取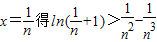
点评:本题主要考查了函数的单调性,以及导数的应用和不等式的证明方法,属于中档题.
(Ⅱ)需要分类讨论,由(Ⅰ)可知分类标准为b≥
 ,0<b<
,0<b< ,b≤0或f'(x)<0.参数取某些特定值时,可只管作出判断,单列为一类;不能作出直观判断的,再分为一类,用通法解决,另外要注意由f'(x)=0求得的根不一定就是极值点,需要判断在该点两侧的异号性后才能称为“极值点”.
,b≤0或f'(x)<0.参数取某些特定值时,可只管作出判断,单列为一类;不能作出直观判断的,再分为一类,用通法解决,另外要注意由f'(x)=0求得的根不一定就是极值点,需要判断在该点两侧的异号性后才能称为“极值点”.(Ⅲ)先构造函数h(x)=x3-x2+ln(x+1),然后研究h(x)在[0,+∞)上的单调性,求出函数h(x)的最小值,从而得到ln(x+1)>x2-x3,最后令
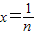 ,即可证得结论.
,即可证得结论.解答:解:(Ⅰ)函数f(x)=x2+bln(x+1)的定义域在(-1,+∞)
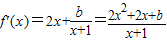
令g(x)=2x2+2x+b,则g(x)在
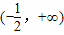 上递增,在
上递增,在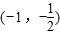 上递减,
上递减,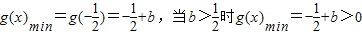
g(x)=2x2+2x+b>0在(-1,+∞)上恒成立,
所以f'(x)>0即当
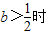 ,函数f(x)在定义域(-1,+∞)上单调递增.
,函数f(x)在定义域(-1,+∞)上单调递增.(Ⅱ)(1)由(Ⅰ)知当
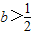 时函数f(x)无极值点
时函数f(x)无极值点(2)当
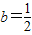 时,
时,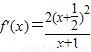 ,
,∴
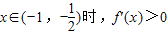
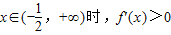 ,
,∴
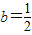 时,函数f(x)在(-1,+∞)上无极值点
时,函数f(x)在(-1,+∞)上无极值点(3)当
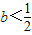 时,解f'(x)=0得两个不同解
时,解f'(x)=0得两个不同解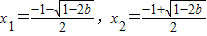
当b<0时,
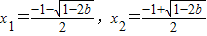 ,
,∴x1∈(-∞,-1),x2∈(-1,+∞),此时f(x)在(-1,+∞)上有唯一的极小值点
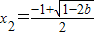
当
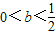 时,x1,x2∈(-1,+∞)f'(x)在(-1,x1),(x2,+∞)都大于0,
时,x1,x2∈(-1,+∞)f'(x)在(-1,x1),(x2,+∞)都大于0,f'(x)在(x1,x2)上小于0,此时f(x)有一个极大值点
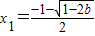 和一个极小值点
和一个极小值点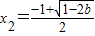
综上可知,b<0,时,f(x)在(-1,+∞)上有唯一的极小值点
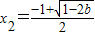
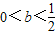 时,f(x)有一个极大值点
时,f(x)有一个极大值点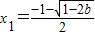 和一个极小值点
和一个极小值点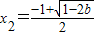
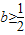 时,函数f(x)在(-1,+∞)上无极值点.
时,函数f(x)在(-1,+∞)上无极值点.(Ⅲ)当b=-1时,f(x)=x2-ln(x+1).令
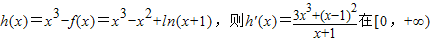 上恒正
上恒正∴h(x)在[0,+∞)上单调递增,
当x∈(0,+∞)时,恒有h(x)>h(0)=0
即当x∈(0,+∞)时,有x3-x2+ln(x+1)>0,ln(x+1)>x2-x3,对任意正整数n,取
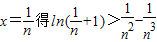
点评:本题主要考查了函数的单调性,以及导数的应用和不等式的证明方法,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目