题目内容
已知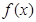 是定义在实数集
是定义在实数集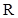 上的奇函数,且当
上的奇函数,且当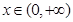 时,
时,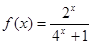
(1)求函数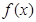 在
在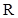 上的解析式;
上的解析式;
(2)判断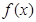 在
在 上的单调性并证明;
上的单调性并证明;
(3)对于任意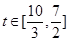 ,不等式
,不等式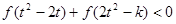 恒成立,求
恒成立,求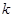 的取值范围.
的取值范围.
【答案】
(1) ;(2)见解析;(3)
;(2)见解析;(3) .
.
【解析】(1)当x∈(- ,0), 则-x∈(0,
,0), 则-x∈(0, ),根据
),根据
同时注意f(0)=0.
(2)要利用单调性的定义来判断.或利用导数也可以.
(3)解本题的关键是把原不等式 转化为
转化为 ,下一步的关键是确定当
,下一步的关键是确定当 时,
时,
结合图像可知 恒成立.进而不等式转化为
恒成立.进而不等式转化为 恒成立问题解决即可.
恒成立问题解决即可.
解:(1)∵f(x)是R上的奇函数,∴ f(0)=0------------------1分
设x∈(- ,0), 则-x∈(0,
,0), 则-x∈(0, ),
),
 -------------3分
-------------3分
 ----------------------4分
----------------------4分
(2)设 ,有
,有
 ------8分
------8分
∵ ,∴
,∴ ,∴
,∴
∴f(x)在( ,0)上为减函数------------------------9分
,0)上为减函数------------------------9分
(3)由 得
得
 ------------------10分
------------------10分
又当 时,
时,
结合图像可知 恒成立,故
恒成立,故 恒成立-------12分
恒成立-------12分
故 ,
,
 --------------------------------15分
--------------------------------15分

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
 是定义在实数集
是定义在实数集 上的增函数,且
上的增函数,且 ,函数
,函数 在
在 上为增函数,在
上为增函数,在 上为减函数,且
上为减函数,且 ,则集合
,则集合 =
=  B、
B、 C、
C、 D、
D、
 是定义在实数集
是定义在实数集 上的奇函数,对任意的实数
上的奇函数,对任意的实数 ,当
,当 时,
时, ,则
,则 等于
等于 B.
B. C.
C. D.
D.
 是定义在实数集上的奇函数,且
是定义在实数集上的奇函数,且 ,给出下列结论:①
,给出下列结论:① ;②
;② 轴对称;④
轴对称;④ .这些结论中正确结论的序号是
.
.这些结论中正确结论的序号是
.