题目内容
已知 ,
, 均为单位向量,其中夹角为θ,有下列四个命题
均为单位向量,其中夹角为θ,有下列四个命题
p1:| +
+ |>1?θ∈[0,
|>1?θ∈[0, ) p2:|
) p2:| +
+ |>1?θ∈(
|>1?θ∈( ,π]
,π]
p3:| -
- |>1?θ∈[0,
|>1?θ∈[0, ) p4:|
) p4:| -
- |>1?θ∈(
|>1?θ∈( ,π]
,π]
其中真命题是
- A.p2,p3
- B.p1,p3
- C.p1,p4
- D.p3,p4
C
分析:利用向量数量积的概念与性质对pi(i=1,2,3,4)逐个判断即可.
解答:∵ ,
, 均为单位向量,其中夹角为θ,
均为单位向量,其中夹角为θ,
∴p1:| +
+ |>1?
|>1? >1?1+1+2
>1?1+1+2 >1?
>1? >-
>- ?cosθ>-
?cosθ>- ,而θ∈[0,π],
,而θ∈[0,π],
∴θ∈[0, ),即p1正确,从而p2错误;
),即p1正确,从而p2错误;
p3:| -
- |>1?
|>1?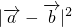 >1?1+1-2
>1?1+1-2 >1?
>1? <
< ?cosθ<
?cosθ< ,而θ∈[0,π],
,而θ∈[0,π],
∴θ∈( ,π],故p3错误,p4正确.
,π],故p3错误,p4正确.
综上所述,p1正确,p4正确.
故选C.
点评:本题考查命题的真假判断与应用,着重考查向量数量积的概念与性质及其应用, >1转化为cosθ>-
>1转化为cosθ>- 是关键,属于中档题.
是关键,属于中档题.
分析:利用向量数量积的概念与性质对pi(i=1,2,3,4)逐个判断即可.
解答:∵
 ,
, 均为单位向量,其中夹角为θ,
均为单位向量,其中夹角为θ,∴p1:|
 +
+ |>1?
|>1? >1?1+1+2
>1?1+1+2 >1?
>1? >-
>- ?cosθ>-
?cosθ>- ,而θ∈[0,π],
,而θ∈[0,π],∴θ∈[0,
 ),即p1正确,从而p2错误;
),即p1正确,从而p2错误;p3:|
 -
- |>1?
|>1?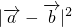 >1?1+1-2
>1?1+1-2 >1?
>1? <
< ?cosθ<
?cosθ< ,而θ∈[0,π],
,而θ∈[0,π],∴θ∈(
 ,π],故p3错误,p4正确.
,π],故p3错误,p4正确.综上所述,p1正确,p4正确.
故选C.
点评:本题考查命题的真假判断与应用,着重考查向量数量积的概念与性质及其应用,
 >1转化为cosθ>-
>1转化为cosθ>- 是关键,属于中档题.
是关键,属于中档题. 
练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目



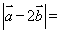












 与
与 均为单位向量,它们的夹角为
均为单位向量,它们的夹角为 ,那么
,那么 等于( )
等于( ) B.
B. C.
C.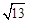 D.4
D.4 与
与 均为单位向量,它们的夹角为
均为单位向量,它们的夹角为 ,则|
,则| |=( )
|=( ) B.
B. C.
C.  D.
D.

 ,
,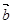 均为单位向量,它们的夹角为
均为单位向量,它们的夹角为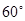 ,则
,则 _______.
_______.