题目内容
已知点P是圆O:![]() 上的任意一点,过P作PD垂直x轴于D,动点Q满足
上的任意一点,过P作PD垂直x轴于D,动点Q满足![]() .
.
⑴求动点Q的轨迹方程;
⑵已知点E(1,1),在动点Q的轨迹上是否存在两个不重合的两点M、N,使![]() (O是坐标原点),若存在,求出直线MN的方程,若不存在,请说明理由.
(O是坐标原点),若存在,求出直线MN的方程,若不存在,请说明理由.
解:⑴设P(![]() ,
,![]() ),Q(x,y),依题意,则点D的坐标为D(
),Q(x,y),依题意,则点D的坐标为D(![]() ,0),
,0),
∴![]() ,
,![]() , (2分)
, (2分)
又![]() ,故
,故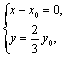 即
即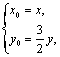 (3分)
(3分)
∵P在圆O上,故有![]() ,
,
∴![]() ,即
,即![]() ,
,
∴点Q的轨迹方程为![]() . (5分)
. (5分)
⑵假设椭圆![]() 上存在不重合的两点M(
上存在不重合的两点M(![]() ,
,![]() ),N(
),N(![]() ,
,![]() )满足
)满足![]() ,
,
则E(1,1)是线段MN的中点,
且有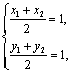 即
即![]() (7分)
(7分)
又M(![]() ,
,![]() ),N(
),N(![]() ,
,![]() )在椭圆
)在椭圆![]() 上,
上,
∴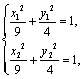 两式相减,得
两式相减,得![]() ,(9分)
,(9分)
∴![]() ,∵点E在椭园内,故故直线MN一定与椭园交于不同两点。故直线MN的方程为4x+9y-13=0.
,∵点E在椭园内,故故直线MN一定与椭园交于不同两点。故直线MN的方程为4x+9y-13=0.
∴椭圆上存在点M,N满足![]() ,此时直线MN的方程为4x+9y-13=0。(12分)
,此时直线MN的方程为4x+9y-13=0。(12分)

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,记动点M的轨迹为曲线C.
,记动点M的轨迹为曲线C. ,问在x轴上是否存在定点E,使得
,问在x轴上是否存在定点E,使得 ?若存在,求出点E的坐标,若不存在,说明理由.
?若存在,求出点E的坐标,若不存在,说明理由.