题目内容
已知a
解:由a2-
得z的实部为正数,z的虚部为负数,
∴复数z的对应点在第四象限.
设z=x+yi(x、y![]() R),则
R),则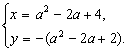
消去a2-
∴复数z对应点的轨迹是一条射线,方程为y=-i+2(x≥3).
点评:根据复数与复平面上点的对应关系知,复数z对应的点在第几象限与复数z的实部和虚部的符号有关.所以本题的关键是判断(a2-
求复数z的对应点的轨迹问题,首先把z表示成z=x+yi(x、y![]() R)的形式,然后寻求x、y之间的关系,但要注意参数限定的条件.
R)的形式,然后寻求x、y之间的关系,但要注意参数限定的条件.
此例是复数与复平面上点的对应概念的练习,学生容易出现的问题是对实部a2-![]() R),转化为求动点(x,y)的轨迹方程.初学时,在这里思维容易混乱,此外在消参数a时,把a2-
R),转化为求动点(x,y)的轨迹方程.初学时,在这里思维容易混乱,此外在消参数a时,把a2-

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目