题目内容
证明:若一个凸多面体的各顶点处的棱数都是奇数,则它的顶点数必是偶数.
证明:设顶点数、面数、棱数分别为V、F、E,则V+F-E=2,
假设顶点数为奇数,
因各顶点处的棱数都是奇数,设为x1,x2,…,xn,
则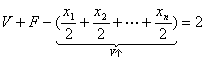
V,
则
.
又∵V为奇数,
∴
不为正整数.
这与已知的棱数为正整数矛盾.∴V为偶数.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
天天向上一本好卷系列答案小学生10分钟应用题系列答案题目内容
证明:若一个凸多面体的各顶点处的棱数都是奇数,则它的顶点数必是偶数.
证明:设顶点数、面数、棱数分别为V、F、E,则V+F-E=2,
假设顶点数为奇数,
因各顶点处的棱数都是奇数,设为x1,x2,…,xn,
则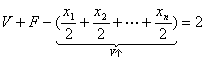V,
则.
又∵V为奇数,
∴不为正整数.
这与已知的棱数为正整数矛盾.∴V为偶数.
天天向上一本好卷系列答案小学生10分钟应用题系列答案