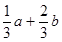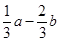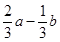题目内容
设二次函数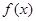 满足:(1)
满足:(1)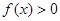 的解集是(0,1);(2)对任意
的解集是(0,1);(2)对任意 都有
都有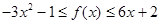 成立。数列
成立。数列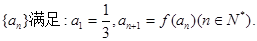
(I)求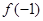 的值;
的值;
(II)求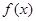 的解析式;
的解析式;
(III)求证: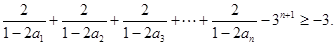
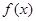 满足:(1)
满足:(1)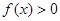 的解集是(0,1);(2)对任意
的解集是(0,1);(2)对任意 都有
都有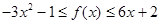 成立。数列
成立。数列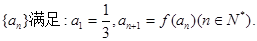
(I)求
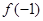 的值;
的值;(II)求
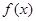 的解析式;
的解析式;(III)求证:
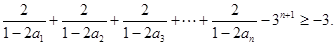
(Ⅰ)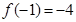 (Ⅱ)
(Ⅱ)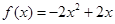
 (Ⅲ)见解析
(Ⅲ)见解析
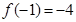 (Ⅱ)
(Ⅱ)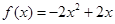
 (Ⅲ)见解析
(Ⅲ)见解析本试题主要是考查了数列的通项公式和二次函数的综合运用。
(1)中由题可知: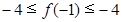 ∴
∴ 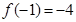
(2)中根据设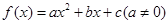 ∵
∵ 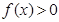 的解集为
的解集为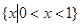
得到参数a,的值。
(3)利用数列的关系式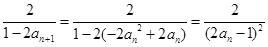
化简变形的得到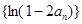 是等比数列.,然后借助于数列的定义和放缩法得到证明
是等比数列.,然后借助于数列的定义和放缩法得到证明
解: (Ⅰ)由题可知: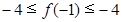 ∴
∴ 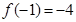 ……2分
……2分
(Ⅱ)设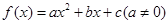 ∵
∵ 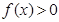 的解集为
的解集为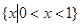
∴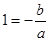 且
且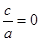 ∴
∴ 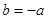 且
且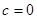 ∴
∴ 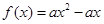
又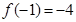 代入
代入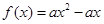 得
得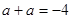 ∴
∴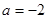
∴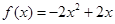
 ……6分
……6分
(Ⅲ)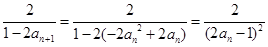 ∴
∴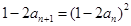
∵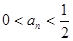 ∴
∴ 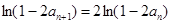 ∴
∴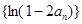 是等比数列.
是等比数列.
∴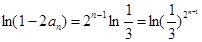 ∴
∴ 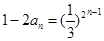 ∴
∴ 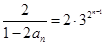
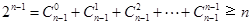 ∴
∴ 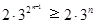
∴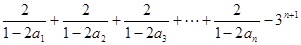
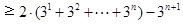
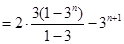
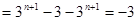 ∴ 原不等式成立
∴ 原不等式成立
(1)中由题可知:
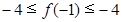 ∴
∴ 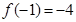
(2)中根据设
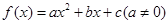 ∵
∵ 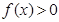 的解集为
的解集为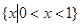
得到参数a,的值。
(3)利用数列的关系式
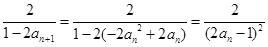
化简变形的得到
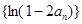 是等比数列.,然后借助于数列的定义和放缩法得到证明
是等比数列.,然后借助于数列的定义和放缩法得到证明解: (Ⅰ)由题可知:
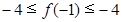 ∴
∴ 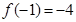 ……2分
……2分(Ⅱ)设
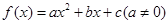 ∵
∵ 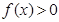 的解集为
的解集为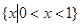
∴
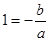 且
且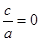 ∴
∴ 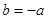 且
且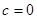 ∴
∴ 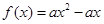
又
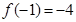 代入
代入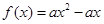 得
得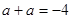 ∴
∴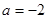
∴
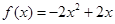
 ……6分
……6分(Ⅲ)
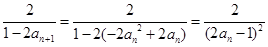 ∴
∴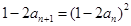
∵
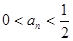 ∴
∴ 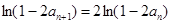 ∴
∴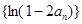 是等比数列.
是等比数列.∴
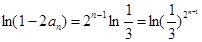 ∴
∴ 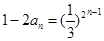 ∴
∴ 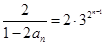
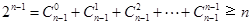 ∴
∴ 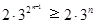
∴
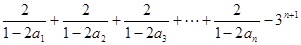
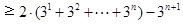
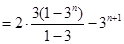
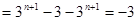 ∴ 原不等式成立
∴ 原不等式成立
练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
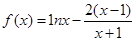 。
。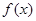 的单调性;
的单调性;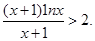
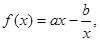 曲线
曲线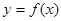 在点
在点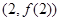 处的切线方程为
处的切线方程为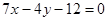 .
.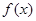 的解析式;
的解析式;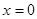 及直线
及直线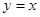 所围成的三角形的面积是一个定值,并求此定值.
所围成的三角形的面积是一个定值,并求此定值.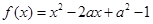 .
.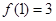 ,求实数
,求实数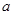 的值;
的值;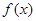 在区间
在区间 上是单调的,求实数
上是单调的,求实数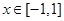 时,求函数
时,求函数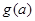 .
.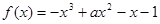 在
在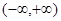 上是单调函数,则实数
上是单调函数,则实数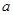 的取值范围是( )
的取值范围是( )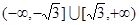
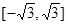
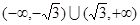
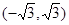
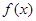 ,若在其定义域内存在两个实数
,若在其定义域内存在两个实数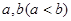 ,使当
,使当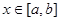 时
时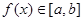 ,则称函数
,则称函数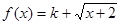 是“Kobe函数”,则实数
是“Kobe函数”,则实数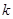 的取值范围是________________
的取值范围是________________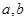 的代数式为
的代数式为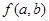 ,它满足关系:
,它满足关系: ; ②
; ②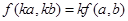 ;
; 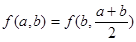 ;④
;④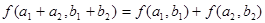 ,
,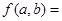 ( )
( )