题目内容
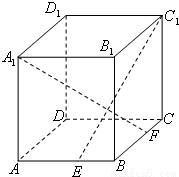
如图,ABCD-A1B1C1D1是正四棱柱,
(1)求证:BD⊥平面ACC1A1;
(2)若二面角C1-BD-C的大小为60°,求异面直线BC1与AC所成角的大小.
(1)求证:BD⊥平面ACC1A1;
(2)若二面角C1-BD-C的大小为60°,求异面直线BC1与AC所成角的大小.

| 解:建立空间直角坐标系D-xyz,如图, (1)设AD=a,DD1=b,则D(0,0,0),A(a,0,0), B(a,a,0),C(0,a,0),C1(0,a,b), ∵  =(-a,-a,0), =(-a,-a,0), =(-a,a,0), =(-a,a,0), =(0,0,b), =(0,0,b),∴  , , , ,∴BD⊥AC,BD⊥CC1, ∵AC,CC1  平面ACC1A1且AC∩CC1=C, 平面ACC1A1且AC∩CC1=C,∴BD⊥平面ACC1A1。 (2)设BD与AC相交于O,则点O坐标为  , , , ,∵  , ,∴BD⊥C1O, 又BD⊥CO, ∴∠C1OC是二面角C1-BD-C的平面角, ∴∠C1OC=60°, ∵  , ,∴  , , ∴cos  = = = = , ,∴异面直线BC1与AC所成角的大小为arccos  。 。 |
 |

练习册系列答案
相关题目
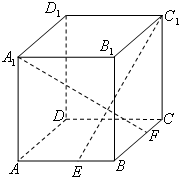 如图,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF.
如图,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF. 如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是 如图,ABCD-A1B1C1D1为正方体,下面结论中正确的结论是
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的结论是