题目内容
设定义在R上的函数f(x)是最小正周期2π的偶函数,f′(x)是函数f(x)的导函数,当x∈[0,π]时,0<f(x)<1; 当x∈(0,π) 且x≠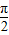 时,(x-
时,(x-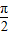 )f′(x)>0,则函数y=f(x)-sinx在[-2π,2π]上的零点个数为( )
)f′(x)>0,则函数y=f(x)-sinx在[-2π,2π]上的零点个数为( )A.2
B.4
C.5
D.8
【答案】分析:根据x∈(0,π) 且x≠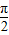 时,(x-
时,(x-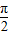 )f′(x)>0,确定函数的单调性,利用函数的图形,即可得到结论.
)f′(x)>0,确定函数的单调性,利用函数的图形,即可得到结论.
解答:解:∵x∈(0,π) 且x≠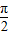 时,(x-
时,(x-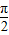 )f′(x)>0
)f′(x)>0
∴x∈(0,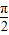 ),函数单调减,x∈(
),函数单调减,x∈(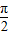 ,π),函数单调增
,π),函数单调增
∵x∈[0,π]时,0<f(x)<1,
在R上的函数f(x)是最小正周期为2π的偶函数,在同一坐标系中作出y=sinx和y=f(x)草图象如下,
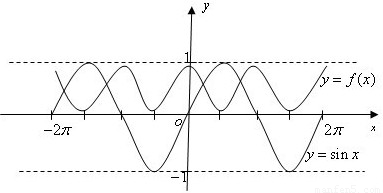
由图知y=f(x)-sinx在[-2π,2π]上的零点个数为4个.
故选B
点评:本题考查函数的单调性,考查函数的零点,考查函数的周期性与奇偶性,属于基础题.
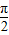 时,(x-
时,(x-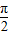 )f′(x)>0,确定函数的单调性,利用函数的图形,即可得到结论.
)f′(x)>0,确定函数的单调性,利用函数的图形,即可得到结论.解答:解:∵x∈(0,π) 且x≠
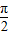 时,(x-
时,(x-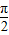 )f′(x)>0
)f′(x)>0∴x∈(0,
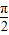 ),函数单调减,x∈(
),函数单调减,x∈(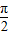 ,π),函数单调增
,π),函数单调增∵x∈[0,π]时,0<f(x)<1,
在R上的函数f(x)是最小正周期为2π的偶函数,在同一坐标系中作出y=sinx和y=f(x)草图象如下,

由图知y=f(x)-sinx在[-2π,2π]上的零点个数为4个.
故选B
点评:本题考查函数的单调性,考查函数的零点,考查函数的周期性与奇偶性,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设定义在R上的函数f(x)同时满足以下条件:①f(x+1)=-f(x)对任意的x都成立;②当x∈[0,1]时,f(x)=ex-e•cos
+m(其中e=2.71828…是自然对数的底数,m是常数).记f(x)在区间[2013,2016]上的零点个数为n,则( )
| πx |
| 2 |
A、m=-
| ||
| B、m=1-e,n=5 | ||
C、m=-
| ||
| D、m=e-1,n=4 |