题目内容
为了解甲、乙两厂的产品质量，采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取14件和5件，测量产品中微量元素x，y的含量(单位：毫克).下表是乙厂的5件产品的测量数据：
| 编号 | 1 | 2 | 3 | 4 | 5 |
| x | 169 | 178 | 166 | 175 | 180 |
| y | 75 | 80 | 77 | 70 | 81 |
(1)已知甲厂生产的产品共98件，求乙厂生产的产品数量；
(2
)当产品中的微量元素x，y满足x≥175且y≥75时，该产品为优等品，用上述样本数据估计乙厂生产的优等品的数量；
(3)从乙厂抽出的上述5件产品中，随机抽取2件，求抽取的2件产品中优等品数ξ的分布列.
(1)由题意知，抽取比例为
＝
，则乙厂生产的产品数量为5×7＝35(件)；
(2)由表格知乙厂生产的优等品为2号和5号，所占比例为
.由此估计乙厂生产的优等品的数量为35×＝14(件)；
(3)由(2)知2号和5号产品为优等品，其余3件为非优等品.ξ的取值为0,1,2.
P(ξ＝0)＝
＝
，P(ξ＝1)＝
＝
＝
，
P(ξ＝2)＝
＝
.
从而分布列为
| ξ | 0 | 1 | 2 |
| P |
|
|
|
| 编号 | 1 | 2 | 3 | 4 | 5 |
| x | 169 | 178 | 166 | 175 | 180 |
| y | 75 | 80 | 77 | 70 | 81 |
（2）当产品中的微量元素x，y满足x≥175，y≥75，该产品为优等品．用上述样本数据估计乙厂生产的优等品的数量．
（3）从乙厂抽出的上述5件产品中，随机抽取2件，求抽取的2件产品中的优等品数ξ的分布列及其均值（即数学期望）．
（2013•昌平区一模）为了解甲、乙两厂的产品的质量，从两厂生产的产品中随机抽取各10件，测量产品中某种元素的含量（单位：毫克）．下表是测量数据的茎叶图：为了解甲、乙两厂的产品质量，采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取12件和5件，测量产品中微量元素x，y的含量（单位：毫克）.下表是乙厂的5件产品的测量数据：
|
编号 |
1 |
2 |
3 |
4 |
5 |
|
x |
169 |
178 |
166 |
175 |
180 |
|
y |
75 |
80 |
77 |
76 |
81 |
（1）已知甲厂生产的产品共84件，求乙厂生产的产品数量；
（2）当产品中的微量元素x，y满足x≥175且y≥75，该产品为优等品，
①用上述样本数据估计乙厂生产的优等品的数量；
②从乙厂抽出的上述5件产品中，随机抽取2件，求抽取的2件产品中优等品数
的分布列及其期望．
为了解甲、乙两厂的产品质量，采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取14件和5件，测量产品中的微量元素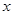
,
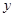的含量（单位：毫克）下表是乙厂的5件产品的测量数据：
|
编号 |
1 |
2 |
3 |
4 |
5 |
|
|
160 |
178 |
166 |
175 |
180 |
|
|
75 |
80 |
77 |
70 |
81 |
（1）已知甲厂生产的产品共有98件，求乙厂生产的产品数量；
（2）若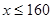
且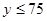
为次品，从乙厂抽出的上述5件产品中，有放回的随机抽取1件产品，抽到次品则停止抽取，否则继续抽取，直到抽出次品为止，但抽取次数最多不超过3次，求抽取次数
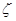的分布列及数学期望.
（本小题满分12分）为了解甲、乙两厂的产品质量，采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取14件和5件，测量产品中的微量元素x，y的含量（单位：毫克）.下表是乙厂的5件产品的测量数据：
|
编号 |
1 |
2 |
3 |
4 |
5 |
|
x |
169 |
178 |
166 |
175 |
180 |
|
y |
75 |
80 |
77 |
70 |
81 |
已知甲厂生产的产品共有98件.
（I）求乙厂生产的产品数量；
（Ⅱ）当产品中的微量元素x，y满足x≥175，且y≥75时，该产品为优等品，用上述样本数据估计乙厂生产的优等品的数量；
（Ⅲ）从乙厂抽出的上述5件产品中，随机抽取2件，求抽取的2件产品中优等品数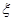
的分布列及其均值（即数学期望）.