题目内容

求证：抛物线y=-1上不存在关于直线x+y=0对称的两点.

证明:假设抛物线y=-1上存在两点P,Q关于直线x+y=0对称,设P（x0,y0）,

则Q（-y0,?-x0）,则有

①-②,得?

y0+x0=,?

即（x0+y0）（x0-y0-2）=0.?

∴x0+y0=0或x0-y0=2.?

若x0+y0=0，则?

P（x0，-x0），Q（x0，-x0）.?

P、Q重合，与题设矛盾.?

若x0-y0=2,代入①式得?

x02-2x0+2=0,?

Δ=（-2）2-4×2=-4＜0,方程无解,?

这样的点不存在.?

故假设不成立,因此抛物线y=-1上不存在两点关于直线x+y=0对称.

练习册系列答案
相关题目
已知椭圆C的中心在原点，焦点在x轴上，它的一个顶点恰好是抛物线y=
1
4
x2的焦点，离心率等于
2
5
5
．
（1）求椭圆C的方程；
（2）过椭圆C的右焦点F作直线l交椭圆C于A、B两点，交y轴于M点，若
MA
=λ1
AF
，
MB
=λ2
BF
，求证：λ1+λ2为定值．
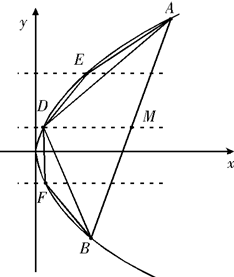（2007•浦东新区二模）已知抛物线C：y2=2px（p＞0）上横坐标为4的点到焦点的距离为5．
（1）求抛物线C的方程．
（2）设直线y=kx+b（k≠0）与抛物线C交于两点A（x1，y1），B（x2，y2），且|y1-y2|=a（a＞0），M是弦AB的中点，过M作平行于x轴的直线交抛物线C于点D，得到△ABD；再分别过弦AD、BD的中点作平行于x轴的直线依次交抛物线C于点E，F，得到△ADE和△BDF；按此方法继续下去．
解决下列问题：
①求证：a2=
16(1-kb)k2
；
②计算△ABD的面积S△ABD；
③根据△ABD的面积S△ABD的计算结果，写出△ADE，△BDF的面积；请设计一种求抛物线C与线段AB所围成封闭图形面积的方法，并求出此封闭图形的面积．
设A（x1，y1）、B（x2，y2）、C（x3，y3）是抛物线y=x2上的三个动点，其中x3＞x2≥0，△ABC是以B为直角顶点的等腰直角三角形．
（1）求证：直线BC的斜率等于x2+x3，也等于
x2-x1x3-x2
；
（2）求A、C两点之间距离的最小值．
求证：抛物线y=-1上不存在关于直线x+y=0对称的两点.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网