题目内容
12.已知等腰△OAB中|OA|=|OB|=2,且$|{\overrightarrow{{O}{A}}+\overrightarrow{{O}{B}}}|≥\frac{{\sqrt{3}}}{3}|{\overrightarrow{{A}{B}}}|$,那么$\overrightarrow{{O}{A}}•\overrightarrow{{O}{B}}$的取值范围是:( )| A. | [-2,4) | B. | (-2,4) | C. | (-4,2) | D. | (-4,2] |
分析 由题意可得,${(\overrightarrow{OA}+\overrightarrow{OB})}^{2}$≥$\frac{1}{3}$${(\overrightarrow{OB}-\overrightarrow{OA})}^{2}$,化简可得$\overrightarrow{OA}•\overrightarrow{OB}$≥-2.再根据$\overrightarrow{OA}•\overrightarrow{OB}$=|$\overrightarrow{OA}$|•|$\overrightarrow{OB}$|•cos∠AOB<4,从而求得$\overrightarrow{{O}{A}}•\overrightarrow{{O}{B}}$的取值范围.
解答 解:由题意等腰△OAB中|OA|=|OB|=2,可得${(\overrightarrow{OA}+\overrightarrow{OB})}^{2}$≥$\frac{1}{3}$${(\overrightarrow{OB}-\overrightarrow{OA})}^{2}$,
化简可得$\overrightarrow{OA}•\overrightarrow{OB}$≥-2.
再根据 $\overrightarrow{OA}•\overrightarrow{OB}$=|$\overrightarrow{OA}$|•|$\overrightarrow{OB}$|•cos∠AOB=2•2•cos∠AOB<4cos∠0=4,
即 $\overrightarrow{OA}•\overrightarrow{OB}$<4.
综上可得,-2≤$\overrightarrow{OA}•\overrightarrow{OB}$<4
故选:A.
点评 本题主要考查两个向量的加减法的法则,以及其几何意义,两个向量的数量积的运算,属于基础题.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案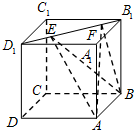 如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=$\frac{1}{2}$,则下列结论中错误的是( )
如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=$\frac{1}{2}$,则下列结论中错误的是( )| A. | AC⊥BE | B. | △AEF的面积与△BEF的面积相等 | ||
| C. | EF∥平面ABCD | D. | 三棱锥A-BEF的体积为定值 |
| 运动时间 (单位:小时) | $[0,\frac{1}{6})$ | $[\frac{1}{6},\frac{1}{3})$ | $[\frac{1}{3},\frac{1}{2})$ | $[\frac{1}{2},\frac{2}{3})$ | $[\frac{2}{3},\frac{5}{6})$ | $[\frac{5}{6},1)$ |
| 总人数 | 10 | 18 | 22 | 25 | 20 | 5 |
(1)根据已知条件完成下面的2×2列联表:
| 课外体育不达标 | 课外体育达标 | 合计 | |
| 男 | |||
| 女 | 10 | 55 | |
| 合计 |
附:${Χ^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| 参考数据 | 当Χ2≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
| 当Χ2>2.706时,有90%的把握判定变量A,B有关联; | |
| 当Χ2>3.841时,有95%的把握判定变量A,B有关联; | |
| 当Χ2>6.635时,有99%的把握判定变量A,B有关联. |
| A. | x-y+1=0 | B. | x-y-3=0 | C. | 2x-y=0 | D. | 2x-y-3=0 |
| A. | $\frac{π}{6}$ | B. | $\frac{π}{12}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
| A. | 3 | B. | $\frac{1}{3}$ | C. | -3 | D. | $-\frac{1}{3}$ |
 已知△ABC中,角A,B,C所对的边分别为a,b,c,若sin2 A+sin2 B=sin2C+sin AsinB,ccosB=b(1-cosC).
已知△ABC中,角A,B,C所对的边分别为a,b,c,若sin2 A+sin2 B=sin2C+sin AsinB,ccosB=b(1-cosC).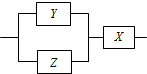 如图,用X、Y、Z这3类不同的元件连接成系统N,每个元件是否正常工作不受其它元件的影响,已知元件X、Y、Z正常工作的概率依次为0.8、0.7、0.9,则系统N正常工作的概率是0.776.
如图,用X、Y、Z这3类不同的元件连接成系统N,每个元件是否正常工作不受其它元件的影响,已知元件X、Y、Z正常工作的概率依次为0.8、0.7、0.9,则系统N正常工作的概率是0.776.