题目内容
数列{an}的通项公式an=ncos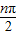 ,其前项和为Sn,则S2013等于( )
,其前项和为Sn,则S2013等于( )A.1006
B.2012
C.503
D.0
【答案】分析:利用数列的通项公式,研究数列前n项和的规律.
解答:解:数列{an}的通项公式an=ncos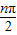 ,
,
所以当n为奇数时,an=0,
当n为偶数时,a2=-2,a4=4,a6=-6,a8=8,
所以S2013=a2+a4+a6+a8+…+a2012
=-2+4-6+8+…-2010+2012
=(-2+4)+(-6+8)+…+(-2010+2012)
=2+2+…+2
=503×2=1006.
故选A.
点评:本题主要考查数列的前n项和,利用数列项的特点发现规律是解决本题的关键,考查学生分析问题的能力,综合性较强.
解答:解:数列{an}的通项公式an=ncos
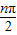 ,
,所以当n为奇数时,an=0,
当n为偶数时,a2=-2,a4=4,a6=-6,a8=8,
所以S2013=a2+a4+a6+a8+…+a2012
=-2+4-6+8+…-2010+2012
=(-2+4)+(-6+8)+…+(-2010+2012)
=2+2+…+2
=503×2=1006.
故选A.
点评:本题主要考查数列的前n项和,利用数列项的特点发现规律是解决本题的关键,考查学生分析问题的能力,综合性较强.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 ,Tn为数列{bn}的前n项和,求Tn.
,Tn为数列{bn}的前n项和,求Tn.