题目内容

半径为4的球面上有A、B、C、D四点，且AB、AC、AD两两互相垂直，则△ABC，△ACD，△ADB面积之和S△ABC+S△ACD+S△ADB的最大值为(    )

A．8                  B．16               C．32                 D．64

答案：C  先补形，如图所示，设AB=a，Ac=b，AD=c，四点A、B、C、D在同一球面上，∴有a2+b2+c2=4R2=4×42，则S△ABC+S△ACD+S△ADB=ab+bc+ca=(ab+bc+ca)≤(a2+ b2+c2)=×43=32(当且仅当a=b=c时取等号)，故选C．

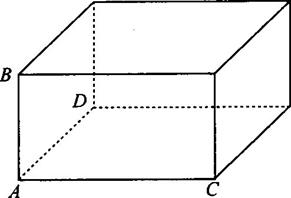
第10题图

练习册系列答案
相关题目
半径为4的球面上有A、B、C、D四点，AB，AC，AD两两互相垂直，则△ABC、△ACD、△ADB面积之和S△ABC+S△ACD+S△ADB的最大值为（　　）
A、8B、16C、32D、64
已知在半径为4的球面上有A、B、C、D四个点，且AB=CD=4，则四面体ABCD体积最大值为（　　）
（2012•桂林一模）半径为4的球面上有A，B，C，D四点，且满足AB⊥AC，AC⊥AD，AD⊥AB，则S△ABC+S△ACD+S△ADB的最大值为（S为三角形的面积）
32
32
．
半径为4的球面上有A、B、C、D四点，且AB、AC、AD两两互相垂直，则△ABC，△ACD，△ADB面积之和的最大值是
32
32
．
半径为4的球面上有A、B、C、D四个点，且满足
AB
?
AC
=0，
AC
?
AD
=0，
AD
?
AB
=0，则S△ABC+S△ACD+S△ADB的最大值为（　　）
A、64B、32C、16D、8

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网