题目内容
已知函数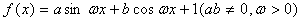
的最小正周期是
，
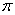有最大值4，且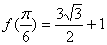
．
（1）求的解析式；
（2）若函数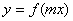
的图象与直线
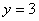的两个相邻交点的距离为
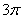，求正数m的值；
（3）若函数
在区间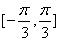
上单调递增，求正数n的取值范围．
【答案】
（1）
， 因为周期
，所以
，
由
得
解得
，
或 
，
（与
矛盾，舍）
所以 
．
（2）因为
的图象与直线
的交点，即为函数
图象上的最大值点，又知两个相邻交点的距离为
，所以函数的最小正
周期为，即有
，
故所求正数
．
（3）因为 
，且
，
所以函数
在
上单调递增，只需
，
由 
求得正数n的取值范围是
．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
的最小正周期为
，将其图象向左平移
个单位长度，所得图象关于
轴对称，则
的一个可能值是
( )
B．
C．
D．
的最小正周期为2π．
，求
的值．
的最小正周期为π，其图象关于直线
对称．
上的单调递增区间；
上只有一个实数解，求实数m的取值范围．
的最小正周期为
.
的值；
的最小正周期为
的值；
在
上恒成立，求实数
的取值范围.