题目内容
9.已知任何一个三次函数f(x)=ax2+bx2+cx+d(a≠0)都有对称中心M(x0,f(x0)),记函数f(x)的导函数为f′(x),f′(x)的导函数为f″(x),则有f″(x0)=0,若函数f(x)=x3-3x2,则$f({\frac{1}{2016}})+f({\frac{2}{2016}})+f({\frac{3}{2016}})+…+f({\frac{4031}{2016}})$=-8062.分析 由题意对已知函数求两次导数可得图象关于点(1,-2)对称,即f(x)+f(2-x)=-4,而要求的式子可用倒序相加法求解,共有2015个-4和一个f(1)=-2,可得答案.
解答 解:依题意,f'(x)=3x2-6x,
∴f''(x)=6x-6.
由f''(x)=0,即6x-6=0,解得x=1,
又 f(1)=-2,
∴f(x)=x3-3x2的对称中心是(1,-2).
即f(x)+f(2-x)=-4.
∴f($\frac{1}{2016}$)+f($\frac{4031}{2016}$)=-4,…f($\frac{2015}{2016}$)+f($\frac{2017}{2016}$)=-4,f($\frac{2016}{2016}$)=-2,
∴$f({\frac{1}{2016}})+f({\frac{2}{2016}})+f({\frac{3}{2016}})+…+f({\frac{4031}{2016}})$=-4×2015+(-2)=-8062
故答案为:-8062.
点评 本题主要考查导数的基本运算,利用条件求出函数的对称中心是解决本题的关键.

练习册系列答案
相关题目
20.函数f(x)=sinx+cosx图象的一个对称轴方程是( )
| A. | x=π | B. | x=$\frac{π}{4}$ | C. | x=$\frac{π}{2}$ | D. | x=$\frac{π}{8}$ |
17.下列通项公式表示的数列为等差数列的是( )
| A. | ${a_n}=\frac{n}{n+1}({n∈{N^*}})$ | B. | ${a_n}={n^2}-1({n∈{N^*}})$ | ||
| C. | ${a_n}=5n+{({-1})^n}({n∈{N^*}})$ | D. | ${a_n}=3n-1({n∈{N^*}})$ |
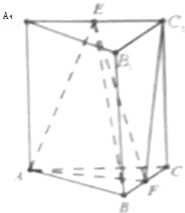 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,E,F分别为A1C1,BC的中点,AA1=3,AC=2,BC=1,AB⊥BC.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,E,F分别为A1C1,BC的中点,AA1=3,AC=2,BC=1,AB⊥BC.