题目内容
函数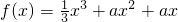 在x=-1处取到极值,那么实数a的值为
在x=-1处取到极值,那么实数a的值为
- A.-2
- B.2
- C.1
- D.以上都不对
D
分析:由函数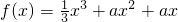 在x=-1处取到极值,故导函数f′(x)=x2+2ax+a在x=-1取到0,由此求出参数的值,再代入到导数中验证,所求出的参数的值是否符合题意.
在x=-1处取到极值,故导函数f′(x)=x2+2ax+a在x=-1取到0,由此求出参数的值,再代入到导数中验证,所求出的参数的值是否符合题意.
解答:∵函数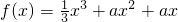
∴f′(x)=x2+2ax+a
∵f′(-1)=0,即1-2a+a=0
∴a=1
但此时f′(x)=x2+2x+1=(x+1)2≥0,函数无极值,
∴x=-1不是极值点,求不出符合条件的参数a的值,
故应选D
点评:本题的考点是利用导数研究函数的极值,考查函数的极值存在时求参数的值,在导数的运用中,利用极值为0处导数为0建立参数求方程,这是导数的一个重要的运用.
分析:由函数
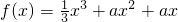 在x=-1处取到极值,故导函数f′(x)=x2+2ax+a在x=-1取到0,由此求出参数的值,再代入到导数中验证,所求出的参数的值是否符合题意.
在x=-1处取到极值,故导函数f′(x)=x2+2ax+a在x=-1取到0,由此求出参数的值,再代入到导数中验证,所求出的参数的值是否符合题意.解答:∵函数
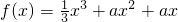
∴f′(x)=x2+2ax+a
∵f′(-1)=0,即1-2a+a=0
∴a=1
但此时f′(x)=x2+2x+1=(x+1)2≥0,函数无极值,
∴x=-1不是极值点,求不出符合条件的参数a的值,
故应选D
点评:本题的考点是利用导数研究函数的极值,考查函数的极值存在时求参数的值,在导数的运用中,利用极值为0处导数为0建立参数求方程,这是导数的一个重要的运用.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
 在x=1处取到极值2
在x=1处取到极值2 ,总存在唯一的
,总存在唯一的 ,使得g(x2)=f(x1),求实数a的取值范围.
,使得g(x2)=f(x1),求实数a的取值范围. 在x=1处取到极值2
在x=1处取到极值2 ,总存在唯一的
,总存在唯一的 ,使得g(x2)=f(x1),求实数a的取值范围.
,使得g(x2)=f(x1),求实数a的取值范围.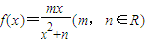 在x=1处取到极值2.
在x=1处取到极值2. .若对任意的x1∈R,总存在x2∈[1,e],使得
.若对任意的x1∈R,总存在x2∈[1,e],使得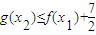 ,求实数a的取值范围.
,求实数a的取值范围.