题目内容
求证:不论x、y取任何非零实数,等式
证明:设存在非零实数x1、y1,使得![]() 成立,?
成立,?
则有y1(x1+y1)+x1(x1+y1)=x1y1,?∴x12+y12+x1y1=0,?
即(x1+![]() )2+
)2+![]() y12=0.?
y12=0.?
但是y1≠0,即(x1+![]() )2+
)2+![]() y12>0,从而得出矛盾,故原命题成立.?
y12>0,从而得出矛盾,故原命题成立.?
点评:正确地作出反设(即否定结论)是正确运用反证法的前提,要注意一些常用的“结论否定形式”,另外,需注意作出的反设必须包括与结论相反的所有情况,也只有证明了与结论相反的所有情况都不成立,才能保证原来的结论一定成立.

练习册系列答案
相关题目
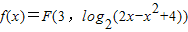 ,写出函数f(x)的定义域;
,写出函数f(x)的定义域;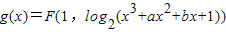 的图象为曲线C,若存在实数b使得曲线C在x(-4<x<-1)处有斜率为-8的切线,求实数a的取值范围
的图象为曲线C,若存在实数b使得曲线C在x(-4<x<-1)处有斜率为-8的切线,求实数a的取值范围 ,写出函数f(x)的定义域;
,写出函数f(x)的定义域; 的图象为曲线C,若存在实数b使得曲线C在x(-4<x<-1)处有斜率为-8的切线,求实数a的取值范围
的图象为曲线C,若存在实数b使得曲线C在x(-4<x<-1)处有斜率为-8的切线,求实数a的取值范围