题目内容
已知函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ< )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为 ,且图象上一个最低点为
,且图象上一个最低点为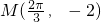 .
.
(1)求f(x)的解析式;
(2)当x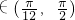 时,f(x)-m≥1恒成立,求实数m的取值范围;
时,f(x)-m≥1恒成立,求实数m的取值范围;
(3)若f(x0)=1,x0∈[-π,π],求x0的值.
解:(1)设周期为T,则由已知可知T=2× =π,
=π,
又ω>0,可知ω=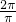 =2,…1分
=2,…1分
又易知A=2,故f(x)=2sin(2x+φ),…2分
∵f( )=-2,
)=-2,
∴sin( +φ)=-1,
+φ)=-1,
∴ +φ=2kπ+
+φ=2kπ+ π(k∈Z),又0<φ<
π(k∈Z),又0<φ< ,
,
解得φ= ,
,
∴f(x)=2sin(2x+ ),…4分
),…4分
(2)当 ≤x≤
≤x≤ 时,
时, ≤2x+
≤2x+ ≤
≤ …5分
…5分
∴- ≤f(x)≤1…6分
≤f(x)≤1…6分
又f(x)≥1+m恒成立,
∴1+m≤- ,解得m≤-
,解得m≤- …8分
…8分
(3)f(x0)=1,则sin(2x0+ )=
)= …9分
…9分
∴2x0+ =2kπ+
=2kπ+ 或2x0+
或2x0+ =2kπ+
=2kπ+ (k∈Z)…10分,
(k∈Z)…10分,
∴x0=kπ或x0=kπ+ (k∈Z),
(k∈Z),
又x0∈[-π,π],
所以x0=-π,- ,0,
,0, ,π…12分
,π…12分
分析:(1)依题意可求得A及其周期T=π,利用周期公式即可求得ω,再利用f( )=-2即可求得φ,从而可求f(x)的解析式;
)=-2即可求得φ,从而可求f(x)的解析式;
(2)由 ≤x≤
≤x≤ ,利用正弦函数的单调性质可求得-
,利用正弦函数的单调性质可求得- ≤f(x)≤1,又f(x)≥1+m恒成立,从而可求得实数m的取值范围;
≤f(x)≤1,又f(x)≥1+m恒成立,从而可求得实数m的取值范围;
(3)f(x0)=1,利用正弦函数的性质即可求得x0的值.
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查函数恒成立问题,考查正弦函数的性质,考查属于难题.
 =π,
=π,又ω>0,可知ω=
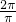 =2,…1分
=2,…1分又易知A=2,故f(x)=2sin(2x+φ),…2分
∵f(
 )=-2,
)=-2,∴sin(
 +φ)=-1,
+φ)=-1,∴
 +φ=2kπ+
+φ=2kπ+ π(k∈Z),又0<φ<
π(k∈Z),又0<φ< ,
,解得φ=
 ,
,∴f(x)=2sin(2x+
 ),…4分
),…4分(2)当
 ≤x≤
≤x≤ 时,
时, ≤2x+
≤2x+ ≤
≤ …5分
…5分∴-
 ≤f(x)≤1…6分
≤f(x)≤1…6分又f(x)≥1+m恒成立,
∴1+m≤-
 ,解得m≤-
,解得m≤- …8分
…8分(3)f(x0)=1,则sin(2x0+
 )=
)= …9分
…9分∴2x0+
 =2kπ+
=2kπ+ 或2x0+
或2x0+ =2kπ+
=2kπ+ (k∈Z)…10分,
(k∈Z)…10分,∴x0=kπ或x0=kπ+
 (k∈Z),
(k∈Z),又x0∈[-π,π],
所以x0=-π,-
 ,0,
,0, ,π…12分
,π…12分分析:(1)依题意可求得A及其周期T=π,利用周期公式即可求得ω,再利用f(
 )=-2即可求得φ,从而可求f(x)的解析式;
)=-2即可求得φ,从而可求f(x)的解析式;(2)由
 ≤x≤
≤x≤ ,利用正弦函数的单调性质可求得-
,利用正弦函数的单调性质可求得- ≤f(x)≤1,又f(x)≥1+m恒成立,从而可求得实数m的取值范围;
≤f(x)≤1,又f(x)≥1+m恒成立,从而可求得实数m的取值范围;(3)f(x0)=1,利用正弦函数的性质即可求得x0的值.
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查函数恒成立问题,考查正弦函数的性质,考查属于难题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目