题目内容
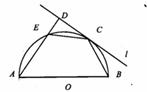
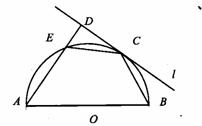
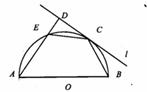
（平面几何选讲）如图，CD是圆O的直径，AE切圆O于点B，连接DB，∠D=20°，则∠DBE的大小为________．
70°
分析：连接CB，利用CD是圆O的直径，AE切圆O于点B，结合弦切角定理，可得结论．
解答：
解：连接CB，则
∵CD是圆O的直径，AE切圆O于点B
∴∠DBE=∠DCB=90°-20°=70°
故答案为：70°
点评：本题考查圆的切线的性质，考查弦切角定理，属于基础题．
分析：连接CB，利用CD是圆O的直径，AE切圆O于点B，结合弦切角定理，可得结论．
解答：
解：连接CB，则∵CD是圆O的直径，AE切圆O于点B
∴∠DBE=∠DCB=90°-20°=70°
故答案为：70°
点评：本题考查圆的切线的性质，考查弦切角定理，属于基础题．
练习册系列答案
相关题目
（平面几何选讲）如图，CD是圆O的直径，AE切圆O于点B，连接DB，∠D=20°，则∠DBE的大小为
过A作直线
的垂线AD，垂足为D，AD交半圆于点E，求证：CB=CE。
过A作直线
的垂线AD，垂足为D，AD交半圆于点E，求证：CB=CE。
过A作直线
的垂线AD，垂足为D，AD交半圆于点E，求证：CB=CE。