题目内容
若关于x的方程
-kx-3+2k=0有且只有两个不同的实数根，则实数k的取值范围是
＜k≤
＜k≤
．
| 4-x2 |
| 5 |
| 12 |
| 3 |
| 4 |
| 5 |
| 12 |
| 3 |
| 4 |
分析：根据方程的根与对应函数的零点的关系，我们可用图象法解答本题，即关于x的方程
-kx-3+2k=0有且只有两个不同的实数根，则函数y=
的图象与y=kx+3-2k的图象有且只有两个交点，在同一坐标系中画出函数y=
的图象与y=kx+3-2k的图象，分析图象即可得到答案．
| 4-x2 |
| 4-x2 |
| 4-x2 |
解答：解：若关于x的方程
-kx-3+2k=0有且只有两个不同的实数根，
则函数y=
的图象与y=kx+3-2k的图象有且只有两个交点
∵函数y=kx+3-2k的图象恒过（2，3）点
故在同一坐标系中画出函数y=
的图象与y=kx+3-2k的图象如下图所示：
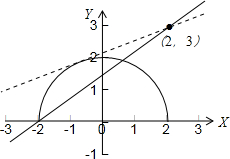
由图可知
当k=
时，直线与圆相切，
当k=
时，直线过半圆的左端点（-2，0）
若函数y=
的图象与y=kx+3-2k的图象有且只有两个交点，则
＜k≤
故答案为：
＜k≤
| 4-x2 |
则函数y=
| 4-x2 |
∵函数y=kx+3-2k的图象恒过（2，3）点
故在同一坐标系中画出函数y=
| 4-x2 |
由图可知
当k=
| 5 |
| 12 |
当k=
| 3 |
| 4 |
若函数y=
| 4-x2 |
| 5 |
| 12 |
| 3 |
| 4 |
故答案为：
| 5 |
| 12 |
| 3 |
| 4 |
点评：本题考查的知识点是根的存在性及根的个数判断，方程的根与函数零点的关系，函数的图象，其中在确定无法解答的方程问题时，将其转化为确定对应函数的零点，利用图象法解答是最常用的方法．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案
相关题目
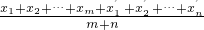的值为
的值为（ ）
的值为（ ）
