题目内容
【题目】已知抛物线
，直线
倾斜角是
且过抛物线
的焦点，直线
被抛物线
截得的线段长是16，双曲线
： 
的一个焦点在抛物线
的准线上，则直线
与
轴的交点
到双曲线
的一条渐近线的距离是（ ）
A. 2 B. 
C. 
D. 1
【答案】D
【解析】抛物线的焦点为
,由弦长计算公式有
,所以抛物线的标线方程为
,准线方程为
,故双曲线的一个焦点坐标为
,即
,所以
,渐近线方程为
,直线
方程为
,所以点
,点P到双曲线的一条渐近线的距离为
,选D.
点睛: 本题主要考查了抛物线与双曲线的简单几何性质, 属于中档题. 先由直线过抛物线的焦点,求出弦长,由弦长求出
的值,根据双曲线中
的关系求出
,渐近线方程等,由点到直线距离公式求出点P到双曲线的一条渐近线的距离.
练习册系列答案
阅读快车系列答案
相关题目
【题目】东莞市某高级中学在今年4月份安装了一批空调，关于这批空调的使用年限
（单位：年， 
）和所支出的维护费用
（单位：万元）厂家提供的统计资料如下：
使用年限 | 1 | 2 | 3 | 4 | 5 |
维护费用 | 6 | 7 | 7.5 | 8 | 9 |
请根据以上数据，用最小二乘法原理求出维护费用
关于
的线性回归方程
；
若规定当维护费用
超过13.1万元时，该批空调必须报废，试根据（1）的结论求该批空调使用年限的最大值.
参考公式：最小二乘估计线性回归方程
中系数计算公式：
， 
， 
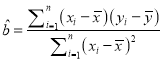