题目内容
已知双曲线的两个焦点为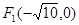
，
，
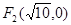是此双曲线上一点，
若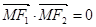
，
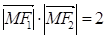，则该双曲线的方程是（ ）
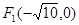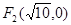，，是此双曲线上一点，若
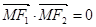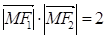，，则该双曲线的方程是（ ）A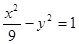． | B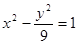． | C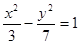． | D． |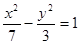
A
分析：由 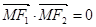，知MF1⊥MF2，所以（|MF1|-|MF2|）2=|MF1|2-2|MF1|?|MF2|+|MF2|2=40-2×2=36，由此得到a=3，进而得到该双曲线的方程．
解答：解：∵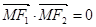
∴
⊥
，∴MF1⊥MF2，
∴|MF1|2+|MF2|2=40，
∴（|MF1|-|MF2|）2=|MF1|2-2|MF1|?|MF2|+|MF2|2=40-2×2=36，
∴||MF1|-|MF2||=6=2a，a=3，
又c=
，∴b2=c2-a2=1，
∴双曲线方程为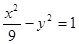
故选A．
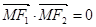，知MF1⊥MF2，所以（|MF1|-|MF2|）2=|MF1|2-2|MF1|?|MF2|+|MF2|2=40-2×2=36，由此得到a=3，进而得到该双曲线的方程．解答：解：∵
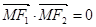
⊥，∴MF1⊥MF2，
∴|MF1|2+|MF2|2=40，
∴（|MF1|-|MF2|）2=|MF1|2-2|MF1|?|MF2|+|MF2|2=40-2×2=36，
∴||MF1|-|MF2||=6=2a，a=3，
又c=
，∴b2=c2-a2=1，∴双曲线方程为
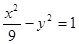
故选A．
练习册系列答案
名校课堂系列答案
相关题目
点
是直线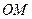
上的一个动点，求当
取最小值时，
的坐标及
的余弦值。
|a|，则a + b与a–b的夹角为（ ）
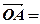a，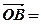
b, 且|a|="|" b|=6，∠AOB=120
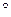，则|a－b|等于（ ）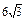
, 
, 且
, 则
( )
, 
，若
，则
________；
＝（0，2，1），
＝（－1，1，－2），则
，若
与
垂直，则
______.
中，
，直线
为BC中垂线，在
，则
▲