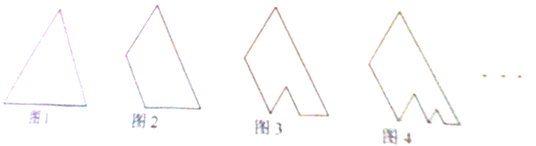题目内容
如图,图1是一块边长为1,面积记为S1的正三角形纸板,沿图1的底边剪去一块边长为 的正三角形纸板后得到图2,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的
的正三角形纸板后得到图2,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的 )后,得图3,图4,…,记第n(n≥3)块纸板的面积为Sn,则Sn-1-Sn= .
)后,得图3,图4,…,记第n(n≥3)块纸板的面积为Sn,则Sn-1-Sn= .
【答案】分析:根据等边三角形的性质得出,三角形的边长,从而可得相邻三角形相似比为:1:2,进而求出相邻三角形面积比,从而可得剪去一块的正三角形纸板面积.
解答:解:∵依次剪去一块更小的正三角形纸板,即其边长为前一块被剪掉正三角形纸板边长的 ,
,
∴剪去三角形的边长分别为: ,
, ,
, …
…
即相邻三角形相似比为:1:2,∴相邻三角形面积比为:1:4,
∴剪去一块的正三角形纸板面积分别为: ,
, ,…
,…
第n个三角形的面积为: ,
,
∴Sn= ,Sn-1=
,Sn-1= ,
,
∴Sn-1-Sn=
故答案为: .
.
点评:本题考查了等边三角形的性质与数据的规律性知识,解题的关键是得出相邻三角形面积比,从而表示出各三角形面积.
解答:解:∵依次剪去一块更小的正三角形纸板,即其边长为前一块被剪掉正三角形纸板边长的
 ,
,∴剪去三角形的边长分别为:
 ,
, ,
, …
…即相邻三角形相似比为:1:2,∴相邻三角形面积比为:1:4,
∴剪去一块的正三角形纸板面积分别为:
 ,
, ,…
,…第n个三角形的面积为:
 ,
,∴Sn=
 ,Sn-1=
,Sn-1= ,
,∴Sn-1-Sn=

故答案为:
 .
.点评:本题考查了等边三角形的性质与数据的规律性知识,解题的关键是得出相邻三角形面积比,从而表示出各三角形面积.

练习册系列答案
相关题目
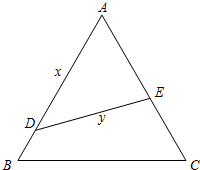 如图,公园内有一块边长为2a的正三角形ABC空地,拟改建成花园,并在其中建一直道DE方便花园管理.设D、E分别在AB、AC上,且DE均分三角形ABC的面积.
如图,公园内有一块边长为2a的正三角形ABC空地,拟改建成花园,并在其中建一直道DE方便花园管理.设D、E分别在AB、AC上,且DE均分三角形ABC的面积.
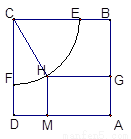
 是一块边长为50m的正方形地皮,扇形
是一块边长为50m的正方形地皮,扇形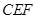 是运动场的一部分,其半径为40m,矩形
是运动场的一部分,其半径为40m,矩形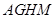 就是拟建的健身室,其中
就是拟建的健身室,其中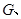
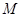 分别在
分别在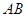 和
和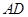 上,
上,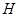 在弧
在弧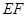 上,设矩形
上,设矩形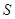 ,∠
,∠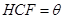 .
.
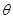 的函数;
的函数; 的正三角形纸板后得到图2,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的
的正三角形纸板后得到图2,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的