题目内容
已知a,b都是负实数,则| a |
| a+2b |
| b |
| a+b |
分析:把所给的式子直接通分相加,把分子整理出含有分母的形式,做到分子常数化,分子和分母同除以分母,把原式的分母变化成具有基本不等式的形式,求出最小值.
解答:解:直接通分相加得
+
=
=1-
=1-
因为a,b都是负实数,所以
,
都为正实数
那么上式中分式中的分母可以利用基本不等式求出最小值
最小值为2
分母有最小值,即
有最大值
那么1-
可得最小值
最小值:2
-2
故答案为:2(
-1).
| a |
| a+2b |
| b |
| a+b |
| a2+2ab+2b2 |
| a2+3ab+2b2 |
=1-
| ab |
| a2+3ab+2b2 |
=1-
| 1 | ||||
|
因为a,b都是负实数,所以
| a |
| b |
| 2b |
| a |
那么上式中分式中的分母可以利用基本不等式求出最小值
最小值为2
| 2 |
分母有最小值,即
| 1 | ||||
|
那么1-
| 1 | ||||
|
最小值:2
| 2 |
故答案为:2(
| 2 |
点评:本题考查函数的最值及其几何意义,本题解题的关键是整理出原式含有基本不等式的形式,可以应用基本不等式求最值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知a,b都是负实数,则
+
的最小值是( )
| a |
| a+2b |
| b |
| a+b |
A、
| ||
B、2(
| ||
C、2
| ||
D、2(
|
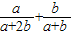 的最小值是 .
的最小值是 .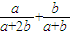 的最小值是( )
的最小值是( )
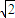 -1)
-1)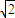 -1
-1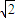 +1)
+1)