题目内容
已知函数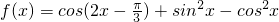 .
.
(I)求函数f(x)的最小正周期及单调递增区间;
(II)设函数 ,求g(x)在区间[0,π]上的最小值及取得最小值时x的值.
,求g(x)在区间[0,π]上的最小值及取得最小值时x的值.
解:(I)∵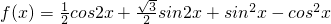
=
=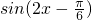 .
.
∴函数的最小正周期 .
.
由 ,
,
得 .
.
即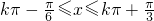 ,
,
∴函数f(x)的单调递增区间为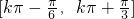 k∈Z.
k∈Z.
(II)∵
而0≤x≤π,所以 .
.
∴当 ,即x=0时,
,即x=0时,
g(x)取得最小值- +2=
+2= .
.
∴g(x)在区间[0,π]上的最小值为 ,取得最小值时x的值为0
,取得最小值时x的值为0
分析:(I)先利用二倍角公式和两角差的正弦公式,将函数f(x)化为y=Asin(ωx+φ)的形式,再利用周期公式求函数的最小正周期,最后利用复合函数单调性结合正弦函数图象求函数的单调区间
(II)先求函数g(x)的解析式,同样化为y=Asin(ωx+φ)的形式,先求内层函数的值域,再结合正弦函数图象求函数的值域即可
点评:本题考查了二倍角公式的运用,两角差的正弦公式及其应用,三角函数的图象和性质,复合函数的单调性和值域
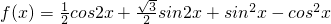
=

=
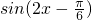 .
.∴函数的最小正周期
 .
.由
 ,
,得
 .
.即
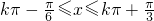 ,
,∴函数f(x)的单调递增区间为
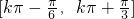 k∈Z.
k∈Z.(II)∵

而0≤x≤π,所以
 .
.∴当
 ,即x=0时,
,即x=0时,g(x)取得最小值-
 +2=
+2= .
.∴g(x)在区间[0,π]上的最小值为
 ,取得最小值时x的值为0
,取得最小值时x的值为0分析:(I)先利用二倍角公式和两角差的正弦公式,将函数f(x)化为y=Asin(ωx+φ)的形式,再利用周期公式求函数的最小正周期,最后利用复合函数单调性结合正弦函数图象求函数的单调区间
(II)先求函数g(x)的解析式,同样化为y=Asin(ωx+φ)的形式,先求内层函数的值域,再结合正弦函数图象求函数的值域即可
点评:本题考查了二倍角公式的运用,两角差的正弦公式及其应用,三角函数的图象和性质,复合函数的单调性和值域

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的 部 分 图 象如 图 所示.
的 部 分 图 象如 图 所示. 的
解 析 式;
的
解 析 式; 中,角
中,角 的
对 边 分 别 是
的
对 边 分 别 是 ,若
,若 的
取 值 范 围.
的
取 值 范 围.