题目内容
1.设x,y,z∈[0,1],求证:(1)x(1-y)+y(1-x)≤1;
(2)x(1-y)+y(1-z)+z(1-x)≤1.
分析 (1)构造函数f(x)=1-[x(1-y)+y(1-x)]=(2y-1)x+1-y,再计算f(0),f(1),结合f(x)的图象,即可得证;
(2)证法一、构造函数f(x)=1-[x(1-y)+y(1-z)+z(1-x)]=(y+z-1)x+(yz+1-y-z),再计算f(0),f(1),结合f(x)的图象,即可得证;
证法二、构造边长为1的正三角形ABC,在AB,BC,AC上分别取D,E,F,使得AD=x,BE=z,CF=y,再由S△ADF+S△BDE+S△CEF<S△ABC,运用面积公式计算即可得证
解答 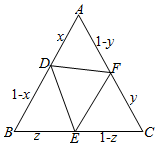 证明:(1)构造函数f(x)=1-[x(1-y)+y(1-x)]=(2y-1)x+1-y
证明:(1)构造函数f(x)=1-[x(1-y)+y(1-x)]=(2y-1)x+1-y
∵x,y∈[0,1],
∴f(0)=1-y≥0,
f(1)=y+(y+1-1-y)=y≥0
由于函数f(x)的图象为一条直线,
则有当0≤x≤1,恒有f(x)≥0成立,
故原不等式成立.
(2)证法一:构造函数f(x)=1-[x(1-y)+y(1-z)+z(1-x)]
=(y+z-1)x+(yz+1-y-z),
∵x,y,z∈[0,1],
∴f(0)=yz+1-y-z=(1-y)(1-z)≥0,
f(1)=y+z-1+(yz+1-y-z)=yz≥0
由于函数f(x)的图象为一条直线,
则有当0≤x≤1,恒有f(x)≥0成立,
故原不等式成立.
证法二:构造边长为1的正三角形ABC,
在AB,BC,AC上分别取D,E,F,使得AD=x,BE=z,CF=y,
则BD=1-x,CE=1-z,AF=1-y,
由于S△ADF+S△BDE+S△CEF≤S△ABC,
即有$\frac{1}{2}$x(1-y)•sin60°+$\frac{1}{2}$z(1-x)•sin60°+$\frac{1}{2}$y(1-z)•sin60°≤$\frac{1}{2}$×1×1×sin60°,
即有x(1-y)+z(1-x)+y(1-z)≤1.
则原不等式成立
点评 本题考查不等式的证明,考查构造法证明不等式的方法:构造函数和构造图形法,考查推理和运算能力,属于中档题.

 初中学业考试导与练系列答案
初中学业考试导与练系列答案| A. | $\frac{π}{4}$ | B. | $1-\frac{π}{4}$ | C. | $\frac{π}{8}$ | D. | $1-\frac{π}{8}$ |
| A. | 2和1 | B. | 2和-1 | C. | 1和-1 | D. | 2和-2 |
| A. | f(x)是偶函数,递增区间是(0,+∞) | B. | f(x)是偶函数,递减区间是(-∞,-1) | ||
| C. | f(x)是奇函数,递增区间是(-∞,-1) | D. | f(x)是奇函数,递增区间是(-1,1) |