题目内容
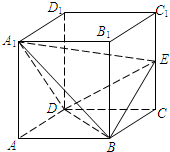 已知正方体ABCD-A1B1C1D1的棱长为2a,若E为棱CC1的中点.
已知正方体ABCD-A1B1C1D1的棱长为2a,若E为棱CC1的中点.(Ⅰ)求证:A1E⊥BD;
(Ⅱ)求二面角A1-BD-E的大小;
(Ⅲ)求四面体A1-BDE的体积.
分析:(I)连接AC,设AC∩DB=O,连接A1O,OE,由正方体的几何特征可得AC为A1E在底面ABCD内的射影,进而由三垂线定理可得A1E⊥BD;
(Ⅱ)由正方体的几何特征可得三角形A1BD为等边三角形,则BD⊥A1O,又BD⊥A1E,由线面垂直的判定定理可得BD⊥平面A1OE,则∠A1OE为二面角A1-BD-E的平面角,解三角形A1OE,即可求出二面角A1-BD-E的大小;
(Ⅲ)由平面A1BD垂直于平面BDE,且A1O⊥BD,由面面垂直的性质,可得A1O⊥平面BDE,即四面体A1-BDE是以三角形BDE为底面,以A1O为高的棱锥,代入棱锥体积公式,即可得到答案.
(Ⅱ)由正方体的几何特征可得三角形A1BD为等边三角形,则BD⊥A1O,又BD⊥A1E,由线面垂直的判定定理可得BD⊥平面A1OE,则∠A1OE为二面角A1-BD-E的平面角,解三角形A1OE,即可求出二面角A1-BD-E的大小;
(Ⅲ)由平面A1BD垂直于平面BDE,且A1O⊥BD,由面面垂直的性质,可得A1O⊥平面BDE,即四面体A1-BDE是以三角形BDE为底面,以A1O为高的棱锥,代入棱锥体积公式,即可得到答案.
解答: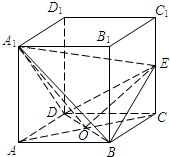 解:(Ⅰ)证明:连接AC,
解:(Ⅰ)证明:连接AC,
设AC∩DB=O,连接A1O,OE,
∵点E在棱CC1上,
∴AC为A1E在底面ABCD内的射影.
由AC⊥BD,
根据三垂线定理,
∴A1E⊥BD. …(3分)
(Ⅱ)在等边三角形A1BD中,BD⊥A1O,又BD⊥A1E,A1O?平面A1OE,A1E?平面A1OE,A1O∩A1E=A1,
∴BD⊥平面A1OE.
于是BD⊥OE,
∴∠A1OE为二面角A1-BD-E的平面角. …(7分)
∵正方体ABCD-A1B1C1D1的棱长为2a,E为棱CC1的中点,
由平面几何知识,得EO=
a
,
满足A1E2=A1O2+EO2,
∴∠A1OE=90°. …(9分)
(Ⅲ)由平面A1BD垂直于平面BDE,且A1O⊥BD,
∴A1O⊥平面BDE.…(12分)
VB-A1DE=VA1-BDE=
S△BDE•A1O=
•
•2
a•
a•
a=2a3.
 解:(Ⅰ)证明:连接AC,
解:(Ⅰ)证明:连接AC,设AC∩DB=O,连接A1O,OE,
∵点E在棱CC1上,
∴AC为A1E在底面ABCD内的射影.
由AC⊥BD,
根据三垂线定理,
∴A1E⊥BD. …(3分)
(Ⅱ)在等边三角形A1BD中,BD⊥A1O,又BD⊥A1E,A1O?平面A1OE,A1E?平面A1OE,A1O∩A1E=A1,
∴BD⊥平面A1OE.
于是BD⊥OE,
∴∠A1OE为二面角A1-BD-E的平面角. …(7分)
∵正方体ABCD-A1B1C1D1的棱长为2a,E为棱CC1的中点,
由平面几何知识,得EO=
| 3 |
|
满足A1E2=A1O2+EO2,
∴∠A1OE=90°. …(9分)
(Ⅲ)由平面A1BD垂直于平面BDE,且A1O⊥BD,
∴A1O⊥平面BDE.…(12分)
VB-A1DE=VA1-BDE=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 6 |
点评:本题考查的知识点是与二面角有关的立体几何综合题,棱锥的体积,空间中直线与直线之间的位置,其中(I)的关键是得到AC为A1E在底面ABCD内的射影,为三垂线定理的使用创造条件;(II)的关键是确定出∠A1OE为二面角A1-BD-E的平面角,(III)的关键是确定出四面体A1-BDE是以三角形BDE为底面,以A1O为高的棱锥.

练习册系列答案
相关题目
 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P在平面DD1C1C内,PD1=PC1=
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P在平面DD1C1C内,PD1=PC1= 已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.
已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.