题目内容
已知:
(其中
是自然对数的底数),
求证:
.
(其中是自然对数的底数),求证:
.见解析
本试题主要是考查了不等式的证明。根据已知指数式不等式可知转换为只要证:
只要证
.(∵
)
然后构造函数
，结合导数的正负得到证明。
证明:∵
∴要证: 
只要证:
只要证.(∵)
取函数,∵
∴当
时,
,∴函数
在
上是单调递减.
∴当时,有
即.得证
只要证
.(∵)然后构造函数
，结合导数的正负得到证明。证明:∵
∴要证: 只要证:
只要证
.(∵)取函数
,∵∴当
时,,∴函数在上是单调递减.∴当
时,有即.得证
练习册系列答案
相关题目
；
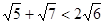的最小值等于
的是( )
，则在① 
，② 
，③ 
，④ 
中，正确的只有
，
，
，
，下列命题：
，
，那么
； ②如果
；
．
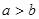，则下列不等式一定正确的是( )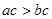
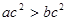
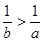
且
，则下列不等式中一定成立的是
＞0，
＞0，
，则A．B的大小关系是 .
，
，
是实数，则下列结论中一定正确的是( )
，则
，则