题目内容
已知函数![]()
![]() (Ⅰ)若函数
(Ⅰ)若函数![]() 在
在![]() 处有极值为10,求b的值;
处有极值为10,求b的值;
(Ⅱ)若对于任意的![]() ,
,![]() 在
在![]() 上单调递增,求b的最小值.
上单调递增,求b的最小值.
(Ⅰ)![]() ,
,
于是,根据题设有
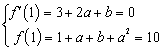
解得![]() 或
或 ![]()
当![]() 时,
时,![]() ,
,![]() ,所以函数有极值点;
,所以函数有极值点;
当![]() 时,
时,![]() ,所以函数无极值点.
,所以函数无极值点.
所以 ![]() .
.
(Ⅱ)法一:![]() 对任意
对任意![]() ,
,![]() 都成立,
都成立,
所以 ![]() 对任意
对任意![]() ,
,![]() 都成立
都成立
因为 ![]() ,
,
所以 ![]() 在
在![]() 上为单调递增函数或为常数函数,
上为单调递增函数或为常数函数,
所以 ![]() 对任意
对任意![]() 都成立
都成立
即 ![]() .
.
又![]() ,
,
所以 当![]() 时,
时,![]() ,
,
所以 ![]() ,
,
所以 ![]() 的最小值为
的最小值为![]() .
.


练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
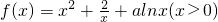 ,
,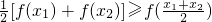 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”. ,
, 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”. ,
, 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.