题目内容
已知关于x的方程(a+2)x2-2ax+a=0有两个不相等的实数根x1和x2,并且抛物线y=x2-(2a+1)x+2a-5于x轴的两个交点分别位于点(2,0)的两旁.
(1)求实数a的取值范围;
(2)当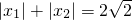 时,求a的值.
时,求a的值.
解:(1)∵方程(a+2)x2-2ax+a=0有两个不相等的实数根x1和x2
∴△=4a2-4a(a+2)=-8a>0,
解得:a<0,
∵抛物线y=x2-(2a+1)x+2a-5于x轴的两个交点分别位于点(2,0)的两旁
∴f(2)<0即f(2)=4-2(2a+1)+2a-5=-2a-3<0,
解得: .
.
综上所述得: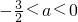 .
.
(2)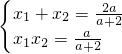 ,
,
∵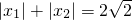
∴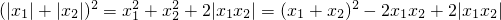 ,
,
①当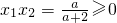 ,
,
即a≥0或a<-2时,
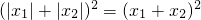 =
=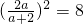 ,
,
解得: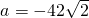 (舍),
(舍),
②当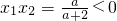 ,
,
即-2<a<0时,
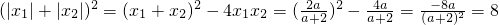 ,
,
解得:a=-4或-1,∵-2<a<0,∴a=-1.
综上所述:a=-1.
分析:(1)由方程(a+2)x2-2ax+a=0有两个不相等的实数根x1和x2,利用根的判断式解得a<0,再由抛物线y=x2-(2a+1)x+2a-5于x轴的两个交点分别位于点(2,0)的两旁,解得: .由此能求出实数a的取值范围.
.由此能求出实数a的取值范围.
(2)由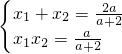 ,知
,知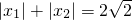 ,由此进行分类讨论,能求出实数a的值.
,由此进行分类讨论,能求出实数a的值.
点评:本题考查实数a的取值范围的求法,考查满足条件的实数值的求法,解题时要认真审题,注意等价转化思想的合理运用.
∴△=4a2-4a(a+2)=-8a>0,
解得:a<0,
∵抛物线y=x2-(2a+1)x+2a-5于x轴的两个交点分别位于点(2,0)的两旁
∴f(2)<0即f(2)=4-2(2a+1)+2a-5=-2a-3<0,
解得:
 .
.综上所述得:
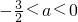 .
.(2)
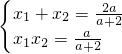 ,
,∵
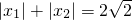
∴
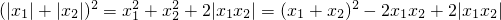 ,
,①当
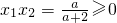 ,
,即a≥0或a<-2时,
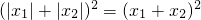 =
=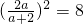 ,
,解得:
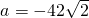 (舍),
(舍),②当
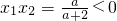 ,
,即-2<a<0时,
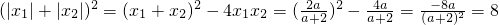 ,
,解得:a=-4或-1,∵-2<a<0,∴a=-1.
综上所述:a=-1.
分析:(1)由方程(a+2)x2-2ax+a=0有两个不相等的实数根x1和x2,利用根的判断式解得a<0,再由抛物线y=x2-(2a+1)x+2a-5于x轴的两个交点分别位于点(2,0)的两旁,解得:
 .由此能求出实数a的取值范围.
.由此能求出实数a的取值范围.(2)由
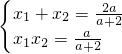 ,知
,知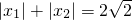 ,由此进行分类讨论,能求出实数a的值.
,由此进行分类讨论,能求出实数a的值.点评:本题考查实数a的取值范围的求法,考查满足条件的实数值的求法,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目