题目内容
设函数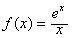 ,
,
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若k>0,求不等式f′(x)+k(1-x)f(x)>0的解集。
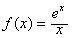 ,
,(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若k>0,求不等式f′(x)+k(1-x)f(x)>0的解集。
解:(Ⅰ) ,
,
由f′(x)=0,得x=1,
因为当x<0时,f′(x)<0;当0<x<1时,f′(x)<0;当x>1时,f′(x)>0;
所以f(x)的单调增区间是:[1,+∞),单调减区间是:(-∞,0),(0,1]。
(Ⅱ)由 ,
,
得(x-1)(kx-1)<0,
故当0<k<1时,解集是 ;
;
当k=1时,解集是 ;
;
当k>1时,解集是 。
。
 ,
,由f′(x)=0,得x=1,
因为当x<0时,f′(x)<0;当0<x<1时,f′(x)<0;当x>1时,f′(x)>0;
所以f(x)的单调增区间是:[1,+∞),单调减区间是:(-∞,0),(0,1]。
(Ⅱ)由
 ,
,得(x-1)(kx-1)<0,
故当0<k<1时,解集是
 ;
;当k=1时,解集是
 ;
;当k>1时,解集是
 。
。
练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目