Question

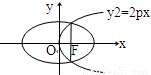
如图所示，已知抛物线y²=2px（p＞0）的焦点恰好是椭圆

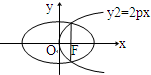
x2

a2

+

y2

b2

=1的右焦点F，且两条曲线的交点连线也过焦点F，则该椭圆的离心率为______．

Answer 1

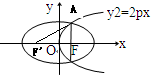
设椭圆的左焦点为F'，抛物线与椭圆在第一象限的交点为A，连接AF'，
∴F（

p

2

，0），F'（-

p

2

，0），可得焦距FF'=p=2c，（c=

a2-b2

为椭圆的半焦距）
对抛物线方程y²=2px令x=

p

2

，得y²=p²，所以AF=|y_A|=p
∴Rt△AFF'中，AF=FF'=p，可得AF'=

2

p
再根据椭圆的定义，可得AF+AF'=2a=（1+

2

）p，
∴该椭圆的离心率为e=

c

a

=

2c

2a

=

p

(1+ 2 )p

=

2

-1
故答案为：

2

-1