题目内容
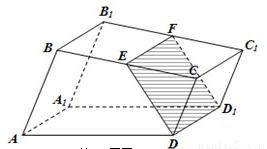
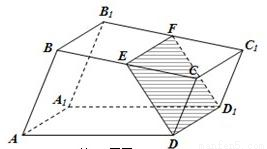
图，已知直四棱柱ABCD-A1B1C1D1的底面是直角梯形，AB⊥BC，AB∥CD，E，F分别是棱BC，B1C1上的动点，且EF∥CC1，CD=DD1=1，AB=2，BC=3。
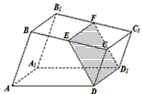
（1）证明：无论点E怎样运动，四边形EFD1D都为矩形；
（2）当EC=1时，求几何体A-EFD1D的体积。
（2）当EC=1时，求几何体A-EFD1D的体积。
解：（1）在直四棱柱
中，
∵
∴
又∵平面
平面
平面
平面
平面
∴
∴四边形
为平行四边形
∵侧棱
底面
，又
平面
内
∴
∴四边形
为矩形；
（2）连结AE
∵四棱柱
为直四棱柱
∴侧棱
底面
又
平面
内
∴
在
中，
，
，则
在
中，
，
，则
在直角梯形
，
∴
即
又∵
∴
平面
由（1）可知，四边形
为矩形，且
，
∴矩形
的面积为
∴几何体
的体积为
。
中，∵
∴
又∵平面
平面平面
平面
平面∴
∴四边形
为平行四边形∵侧棱
底面，又平面内∴
∴四边形
为矩形；（2）连结AE
∵四棱柱
为直四棱柱∴侧棱
底面又
平面内∴
在
中，，，则在
中，，，则在直角梯形
，∴
即
又∵
∴
平面由（1）可知，四边形
为矩形，且，∴矩形
的面积为∴几何体
的体积为。
练习册系列答案
津桥教育计算小状元系列答案
相关题目
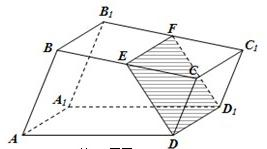如图，已知直四棱柱ABCD-A1B1C1D1的底面是直角梯形，AB⊥BC，AB∥CD，E，F分别是棱BC，B1C1上的动点，且EF∥CC1，CD=DD1=1，AB=2，BC=3．
