题目内容
已知数列{an}的前n项和为Sn,Sn=n2+n,数列{ }的前n项和Tn=
}的前n项和Tn=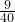 则n=
则n=
- A.1
- B.8
- C.9
- D.10
C
分析:由题意先有数列的前n项和 Sn=n2+n得到数列an的通项公式,再有通项公式利用裂项相消法求解即可
解答:∵数列{an}的前n项和 Sn=n2+n,
∴ ?an=2n,
?an=2n,
即 =
= =
= =
=
有要求和的数列的通项公式特点选择裂项相消可以得到:
 =
= .
.
令Tn=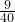 则n=9.
则n=9.
故答案为:C
点评:此题考查了有数列的前n项和求通项,数列的裂项相消法求其前n项的和.
分析:由题意先有数列的前n项和 Sn=n2+n得到数列an的通项公式,再有通项公式利用裂项相消法求解即可
解答:∵数列{an}的前n项和 Sn=n2+n,
∴
 ?an=2n,
?an=2n,即
 =
= =
= =
=
有要求和的数列的通项公式特点选择裂项相消可以得到:
 =
= .
.令Tn=
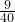 则n=9.
则n=9.故答案为:C
点评:此题考查了有数列的前n项和求通项,数列的裂项相消法求其前n项的和.

练习册系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |