题目内容
(本小题满分12分)
已知![]() .
.
(Ⅰ)已知对于给定区间![]() ,存在
,存在![]() 使得
使得![]() 成立,求证:
成立,求证:![]() 唯一;
唯一;
(Ⅱ)若![]() ,当
,当![]() 时,比较
时,比较![]() 和
和![]() 大小,并说明理由;
大小,并说明理由;
(Ⅲ)设A、B、C是函数![]() 图象上三个不同的点,
图象上三个不同的点,
求证:△ABC是钝角三角形.
(本小题满分12分)
解:(Ⅰ)证明:假设存在![]()
![]() ,
,![]() ,即
,即![]() . 1分
. 1分
∵![]() ,∴
,∴![]() 上的单调增函数(或者通过复合函数单调性说明
上的单调增函数(或者通过复合函数单调性说明![]() 的单调性). 3分
的单调性). 3分
∴![]() 矛盾,即
矛盾,即![]() 是唯一的. 4分
是唯一的. 4分
(Ⅱ) ![]() 原因如下:
原因如下:
(法一)设![]() 则
则
![]()
![]()
![]() . 5分
. 5分
∵![]() . 6分
. 6分
∴1+![]() ,
,
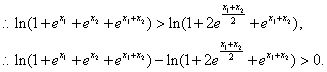
![]() . 8分
. 8分
(法二)设![]() ,则
,则![]() .
.
由(Ⅰ)知![]() 单调增.
单调增.
所以当![]() 即
即![]() 时,有
时,有![]()
所以![]() 时,
时,![]() 单调减. 5分
单调减. 5分
当![]() 即
即![]() 时,有
时,有![]()
所以![]() 时,
时,![]() 单调增. 6分
单调增. 6分
所以![]() ,所以
,所以![]() . 8分
. 8分
(Ⅲ)证明:设![]() ,因为
,因为![]()
∵![]() 上的单调减函数. 9分
上的单调减函数. 9分
∴![]() .∵
.∵![]()
∴![]() . 10分
. 10分
∵![]()
∴![]() 为钝角. 故△
为钝角. 故△![]() 为钝角三角形. 12分
为钝角三角形. 12分

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
相关题目