题目内容
已知函数
，f（2）=1．
（1）求a的值； （2）求证：函数f（x）在（-∞，0）内是减函数．
解：（1）由已知，得
，
∴a=2．…
证明：（2）由（1）得
，
设任意x1，x2∈（-∞，0），且x1＜x2．
则
．…
∵x1，x2∈（-∞，0），且x1＜x2．
∴x2-x1＞0，x1x2＞0，
∴f（x1）-f（x2）＞0，即f（x1）＞f（x2）．
所以，函数f（x）在（-∞，0）内是减函数．…
分析：（1）由已知f（2）=1可求a
（2）由（1）得，利用单调性的定义，设任意x1，x2∈（-∞，0），且x1＜x2．判断的符号即可证明
点评：本题主要考查了利用待定系数法求解函数解析式，函数单调性的定义在证明单调性中的应用，属于基础试题
，∴a=2．…
证明：（2）由（1）得
，设任意x1，x2∈（-∞，0），且x1＜x2．
则
．…∵x1，x2∈（-∞，0），且x1＜x2．
∴x2-x1＞0，x1x2＞0，
∴f（x1）-f（x2）＞0，即f（x1）＞f（x2）．
所以，函数f（x）在（-∞，0）内是减函数．…
分析：（1）由已知f（2）=1可求a
（2）由（1）得
，利用单调性的定义，设任意x1，x2∈（-∞，0），且x1＜x2．判断的符号即可证明点评：本题主要考查了利用待定系数法求解函数解析式，函数单调性的定义在证明单调性中的应用，属于基础试题
练习册系列答案
相关题目
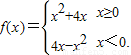若f（2-a2）＞f（a），则实数a的取值范围是（ ）
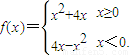若f（2-a2）＞f（a），则实数a的取值范围是（ ）
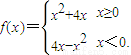若f（2-a2）＞f（a），则实数a的取值范围是（ ）
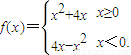若f（2-a2）＞f（a），则实数a的取值范围是（ ）