题目内容
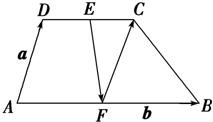如图，已知梯形ABCD中，AB∥CD，且AB=2CD，E、F分别是DC、AB的中点，设| AD |
| a |
| AB |
| b |
| a |
| b |
| DC |
| EF |
| FC |
分析：根据题意知，
=
，
=
，并且有
=
，分别求出
和
；再由三角形法则对应的首尾相连法则得
=
+
+
，结合图形和题意用
和
表示出来．
| FC |
| AD |
| DC |
| AF |
| AF |
| 1 |
| 2 |
| AB |
| FC |
| DC |
| EF |
| ED |
| DA |
| AF |
| a |
| b |
解答：解：∵DC∥AB，AB=2DC，E、F分别是DC、AB的中点，
∴
=
=
，
=
=
=
．
∴
=
+
+
=-
-
+
=-
×
-
+
=
-
．
∴
| FC |
| AD |
| a |
| DC |
| AF |
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
| b |
∴
| EF |
| ED |
| DA |
| AF |
=-
| 1 |
| 2 |
| DC |
| AD |
| 1 |
| 2 |
| AB |
=-
| 1 |
| 2 |
| 1 |
| 2 |
| b |
| a |
| 1 |
| 2 |
| b |
| 1 |
| 4 |
| b |
| a |
点评：本题考查了向量加法以及几何意义的应用，主要是结合图形和题意对向量进行转化，即用已知向量来表示未知向量．
练习册系列答案
相关题目
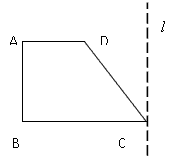
如图，已知梯形ABCD中，AD∥BC，∠ABC=90°，AD=a，BC=2a，∠DCB=60°，在平面ABCD内，过C作l⊥CB，以l为轴将梯形ABCD旋转一周，求所得旋转体的表面积及体积．
＝λ
(λ∈R，λ＞0)．
时，求证：GM∥平面DFN．
，试求二面角M－BC－D的余弦值．
为矩阵
属于λ的一个特征向量，求实数a，λ的值及A2。
（α为参数），曲线D的参数方程为
，（t为参数）。若曲线C、D有公共点，求实数m的取值范围。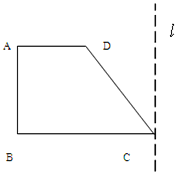
如图，已知梯形ABCD中，AD∥BC，∠ABC=90°，AD=a，BC=2a，∠DCB=60°，在平面ABCD内，过C作l⊥CB，以l为轴将梯形ABCD旋转一周，求所得旋转体的表面积及体积．