题目内容
已知m,n,t均为实数,[u]表示不超过实数u的最大整数,若
≤0对任意实数x恒成立,且m(1-P)+n(1+P)+t=0(n>m>0),则实数P的最大值为______.
| mx2+nx+t |
| -x+[x]-2 |
由题意知:
对任意实数X恒成立
∵[x]≤x∴分母-x+[x]-2必小于0
即对任意实数x恒成立.
所以n2-4mt≤0
即
≥
而n>m>0 所以 t>0;
-1<0
又P=
=
≤
=
=
(*)
令s=
故s>1
∴(*)=
=-
=-
=-[
(s-1)+
•
]-
≤-2
-
=-3
故答案为-3
对任意实数X恒成立
∵[x]≤x∴分母-x+[x]-2必小于0
即对任意实数x恒成立.
所以n2-4mt≤0
即
| t |
| n |
| n |
| 4m |
而n>m>0 所以 t>0;
| m |
| n |
又P=
| m+n+t |
| m-n |
| ||||
|
| ||||
|
m2+mn+
| ||
| m2-mn |
1+
| ||||||
1-
|
令s=
| n |
| m |
∴(*)=
1+s+
| ||
| 1-s |
1+s+
| ||
| s-1 |
| ||||||
| s-1 |
=-[
| 1 |
| 4 |
| 9 |
| 4 |
| 1 |
| s-1 |
| 3 |
| 2 |
≤-2
|
| 3 |
| 2 |
故答案为-3

练习册系列答案
相关题目
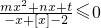 对任意实数x恒成立,且m(1-P)+n(1+P)+t=0(n>m>0),则实数P的最大值为________.
对任意实数x恒成立,且m(1-P)+n(1+P)+t=0(n>m>0),则实数P的最大值为________.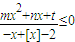 对任意实数x恒成立,且m(1-P)+n(1+P)+t=0(n>m>0),则实数P的最大值为 .
对任意实数x恒成立,且m(1-P)+n(1+P)+t=0(n>m>0),则实数P的最大值为 .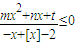 对任意实数x恒成立,且m(1-P)+n(1+P)+t=0(n>m>0),则实数P的最大值为 .
对任意实数x恒成立,且m(1-P)+n(1+P)+t=0(n>m>0),则实数P的最大值为 .