题目内容
已知函数f(x)=lnx-px+1(p∈R).(1)p=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求函数f(x)的极值;
(3)若对任意的x>0,恒有f(x)≤p2x2,求实数p的取值范围.
【答案】分析:(1)求出切线斜率,切点坐标,可得曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求导数,分类讨论,确定函数的单调性,从而可求函数f(x)的极值;
(3)记g(x)=f(x)-p2x2=lnx-px+1-p2x2(x>0),求导数,分类讨论,确定g(x)的最大值,解不等式,可求p的取值范围.
解答:解:(1)p=1,f'(1)=1-1=0,f(1)=0-1+1=0,∴曲线y=f(x)在点(1,f(1))处的切线方程为:y=0(2分)
(2)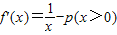
当p≤0时,f'(x)>0,f(x)在(0,+∞)上递增,函数f(x)无极值; (4分)
当p>0时,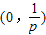 上f'(x)>0,f(x)单调递增;
上f'(x)>0,f(x)单调递增;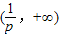 上f'(x)<0,f(x)单调递减
上f'(x)<0,f(x)单调递减
∴f(x)的极大值为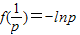 ,f(x)无极小值 (6分)
,f(x)无极小值 (6分)
(3)记g(x)=f(x)-p2x2=lnx-px+1-p2x2(x>0)
∴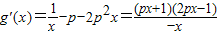 (7分)
(7分)
当p=0时,g(x)=lnx+1,g(e)>0不符合条件 (8分)
当p>0时,px+1>0,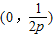 上g'(x)>0,g(x)单调递增;
上g'(x)>0,g(x)单调递增;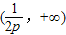 上g'(x)<0,g(x)单调递减
上g'(x)<0,g(x)单调递减
∴g(x)的最大值为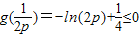 ,∴
,∴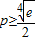 (10分)
(10分)
当p<0时,2px-1<0,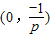 上g'(x)>0,g(x)单调递增;
上g'(x)>0,g(x)单调递增;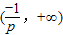 上g'(x)<0,g(x)单调递减
上g'(x)<0,g(x)单调递减
∴g(x)的最大值为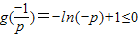 ,∴p≤-e
,∴p≤-e
故p的取值范围是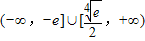 (12分)
(12分)
点评:本题考查导数知识的运用,考查导数的几何意义,考查函数的极值,考查函数的最值,考查分类讨论的数学思想,正确求导与分类是关键.
(2)求导数,分类讨论,确定函数的单调性,从而可求函数f(x)的极值;
(3)记g(x)=f(x)-p2x2=lnx-px+1-p2x2(x>0),求导数,分类讨论,确定g(x)的最大值,解不等式,可求p的取值范围.
解答:解:(1)p=1,f'(1)=1-1=0,f(1)=0-1+1=0,∴曲线y=f(x)在点(1,f(1))处的切线方程为:y=0(2分)
(2)
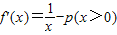
当p≤0时,f'(x)>0,f(x)在(0,+∞)上递增,函数f(x)无极值; (4分)
当p>0时,
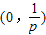 上f'(x)>0,f(x)单调递增;
上f'(x)>0,f(x)单调递增;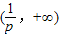 上f'(x)<0,f(x)单调递减
上f'(x)<0,f(x)单调递减∴f(x)的极大值为
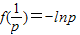 ,f(x)无极小值 (6分)
,f(x)无极小值 (6分)(3)记g(x)=f(x)-p2x2=lnx-px+1-p2x2(x>0)
∴
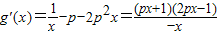 (7分)
(7分)当p=0时,g(x)=lnx+1,g(e)>0不符合条件 (8分)
当p>0时,px+1>0,
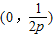 上g'(x)>0,g(x)单调递增;
上g'(x)>0,g(x)单调递增;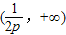 上g'(x)<0,g(x)单调递减
上g'(x)<0,g(x)单调递减∴g(x)的最大值为
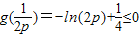 ,∴
,∴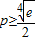 (10分)
(10分)当p<0时,2px-1<0,
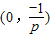 上g'(x)>0,g(x)单调递增;
上g'(x)>0,g(x)单调递增;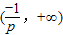 上g'(x)<0,g(x)单调递减
上g'(x)<0,g(x)单调递减∴g(x)的最大值为
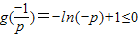 ,∴p≤-e
,∴p≤-e故p的取值范围是
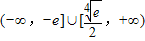 (12分)
(12分)点评:本题考查导数知识的运用,考查导数的几何意义,考查函数的极值,考查函数的最值,考查分类讨论的数学思想,正确求导与分类是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目