题目内容
已知函数f(x)＝－ 
＋ 
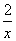(x>0)．
(1)解关于x的不等式f(x)>0；(2)若f(x)＋2x≥0在(0，＋∞)上恒成立，求a的取值范围．
解：(1)不等式f(x)>0，即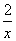－＋>0，即
>0.整理成(x－2a)·ax<0.①当a>0时，不等式x(x－2a)<0，
不等式的解为0<x<2a.②当a<0时，不等式x(x－2a)>0，不等式的解为x>0或x<2a(舍去)．综上，a>0时，不等式解集为{x|0<x<2a}，a<0时，解集为{x|x>0}．
(2)若f(x)＋2x≥0在(0，＋∞)上恒成立，即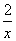－＋＋2x≥0，∴≤2
.∵2的最小值为4，故≤4，解得a<0或a≥
.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，若存在实数
，使得
成立，则实数
的取值范围是( ) w
B．
C．
D．
，则实数a的取值范围为 。 
{1,2,3,4,5}，且若a∈S，则必有6－a∈S，则所有满足上述条件的集合S共有（ ）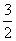
，且g（x）＝a2x＋a－2x－2mf（x）在[1，＋∞）上的最小值为－2，求m的值．
是奇函数
的值，并求该函数的定义域； （Ⅱ）根据（Ⅰ）的结果，判断
在
上的单调性，并给出证明. 
R }则a+b＝
C、
D、
,命题
：实数
为小于6的正整数，命题
：A是B成立的必要不充分条件.若命题
是真命题，求实数