题目内容
数列{an}:a1,a2,a3,…,an,…,构造一新数列:a1,(a2-a1),(a3-a2),…,(an-an-1),….此数列是首项为1,公比为(1)求{an}的通项an;
(2)求{an}的前n项和Sn.
解:(1)an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=1+ (2)Sn=a1+a2+a3+…+an= 所以Sn=
![]() +(
+(![]() )2+…+(
)2+…+(![]() )n-1=
)n-1=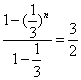 [1-(
[1-(![]() )n].
)n].![]() (1-
(1-![]() )+
)+ ![]() [1-(
[1-(![]() )2]+
)2]+![]() [1-(
[1-(![]() )3]+…+
)3]+…+![]() [1-(
[1-(![]() )n],
)n],![]() {n-
{n-![]() [1+
[1+![]() +(
+(![]() )2+…+(
)2+…+(![]() )n-1]}=
)n-1]}=![]() n-
n-![]() ·
·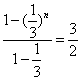 n-
n-![]() [1-(
[1-(![]() )n]=
)n]=![]() (2n-1)+
(2n-1)+![]() (
(![]() )n-1.
)n-1. 练习册系列答案
练习册系列答案
西城学科专项测试系列答案
小考必做系列答案
小考实战系列答案
小考复习精要系列答案
小考总动员系列答案
小升初必备冲刺48天系列答案
68所名校图书小升初高分夺冠真卷系列答案
伴你成长周周练月月测系列答案
小升初金卷导练系列答案
萌齐小升初强化模拟训练系列答案
相关题目
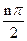 )an+sin
)an+sin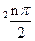 ,n=1.2.3…
,n=1.2.3…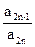 ,令 Sn=
,令 Sn=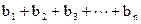 ,求 Sn
,求 Sn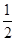 an-1+1 (n≥2)
an-1+1 (n≥2)  )an+sin
)an+sin ,n=1.2.3…
,n=1.2.3… ,令 Sn=
,令 Sn= ,求 Sn
,求 Sn