题目内容
如图所示,已知圆![]() 为圆上一动点,点P在AM上,点N在CM上,且满足
为圆上一动点,点P在AM上,点N在CM上,且满足![]() ,点N的轨迹为曲线E。
,点N的轨迹为曲线E。
(Ⅰ)求曲线E的方程;
(Ⅱ)若过定点F(0,2)的直线交曲线E于不同的两点G、H(点G在点F、H之间),且满足![]() 的取值范围。
的取值范围。

解:(I)![]()
∴NP为AM的垂直平分线,
![]()
又![]()
∴动点N的轨迹是以点C(-1,0),A(1,0)为焦点的椭圆
且椭圆长轴长为![]()
![]()
∴曲线E的方程为![]() …………4分
…………4分
(II)当直线GH斜率存在时,
设直线CH方程为![]()
代入椭圆方程![]() ,
,
得![]()
![]() …………6分
…………6分
设![]()
则
又![]()
![]()
![]()


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013•潮州二模)如图所示,已知AB为圆O的直径,点D为线段AB上一点,且AD=
(2013•潮州二模)如图所示,已知AB为圆O的直径,点D为线段AB上一点,且AD=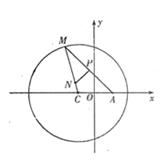 如图所示,已知圆
如图所示,已知圆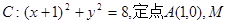 为圆上一动点,点
为圆上一动点,点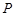 是线段
是线段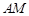 的垂直平分线与直线
的垂直平分线与直线 的交点.
的交点.
 的方程;
的方程;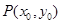 是曲线
是曲线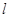 的方程;(不要求证明)
的方程;(不要求证明)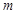 过切点
过切点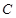 关于直线
关于直线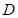 ,证明:直线
,证明:直线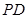 恒过一定点,并求定点的坐标.
恒过一定点,并求定点的坐标.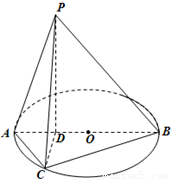 如图所示,已知AB为圆O的直径,点D为线段AB上一点,且AD=
如图所示,已知AB为圆O的直径,点D为线段AB上一点,且AD= DB,点C为圆O上一点,且BC=
DB,点C为圆O上一点,且BC=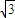 AC.点P在圆O所在平面上的正投影为点D,PD=DB.
AC.点P在圆O所在平面上的正投影为点D,PD=DB.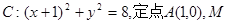 为圆上一动点,点
为圆上一动点,点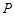 在
在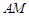 上,点
上,点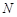 在
在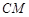 上,且满足
上,且满足 的轨迹为曲线
的轨迹为曲线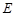 。
。
 求曲线
求曲线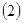 若过定点F(0,2)的直线交曲线
若过定点F(0,2)的直线交曲线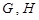 (点
(点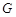 在点
在点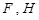 之间),且满足
之间),且满足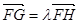 ,求
,求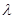 的取值范围。
的取值范围。