题目内容
已知数列{an}的前n项和为Sn，且满足：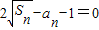
，求数列{an}的通项．
【答案】分析：由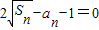
得
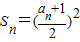当n≥2时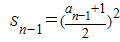
，两式相减，得出数列的递推公式，再根据递推公式去推证数列的性质，求解通项．
解答：解：由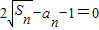
得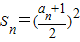
①，
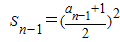当n≥2
②，
①-②得an=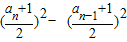
，化简整理得出
（an+an-1）（an-an-1-2）=0
由已知，Sn＞0，所以an＞0，an+an-1≠0，
an-an-1-2=0，由等差数列的定义可知数列{an}是以2为公差的等差数列，
在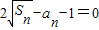
中，令n=1，得2
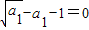，解得a1=1，
所以数列{an}的通项an=1+（n-1）×2=2n-1
点评：本题考查数列的递推公式，通项公式．考查转化构造，推理论证，运算求解能力．
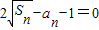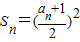得当n≥2时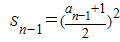，两式相减，得出数列的递推公式，再根据递推公式去推证数列的性质，求解通项．解答：解：由
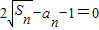
得
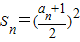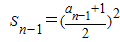①，当n≥2
②，①-②得an=
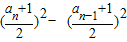，化简整理得出（an+an-1）（an-an-1-2）=0
由已知，Sn＞0，所以an＞0，an+an-1≠0，
an-an-1-2=0，由等差数列的定义可知数列{an}是以2为公差的等差数列，
在
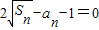中，令n=1，得2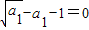，解得a1=1，所以数列{an}的通项an=1+（n-1）×2=2n-1
点评：本题考查数列的递推公式，通项公式．考查转化构造，推理论证，运算求解能力．
练习册系列答案
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn（a、b∈R），且S25=100，则a12+a14等于（ ）
| A、16 | B、8 | C、4 | D、不确定 |