题目内容
已知函数f(x)=ex(x2+ax-a),其中a是常数,
(1)当a=1时,求f(x)在点(1,f(1))处的切线方程;
(2)求f(x)在区间[0,+∞)上的最小值。
(1)当a=1时,求f(x)在点(1,f(1))处的切线方程;
(2)求f(x)在区间[0,+∞)上的最小值。
(1 )由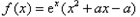 可得
可得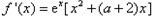 ,
,
当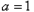 时,
时,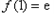 ,
,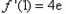 ,
,
所以 曲线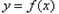 在点
在点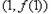 处的切线方程为
处的切线方程为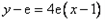 ,即
,即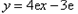 。
。
(2)令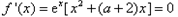 ,解得
,解得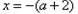 或
或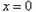 ,
,
当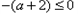 ,即
,即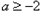 时,在区间
时,在区间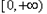 上,
上,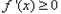 ,
,
所以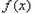 是
是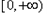 上的增函数,
上的增函数,
所以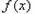 的最小值为
的最小值为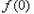 =
=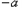 ;
;
当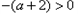 ,即
,即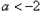 时,
时,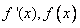 随
随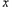 的变化情况如下表
的变化情况如下表

由上表可知函数f(x)的最小值为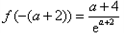 。
。
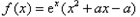 可得
可得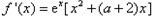 ,
,当
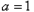 时,
时,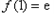 ,
,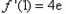 ,
,所以 曲线
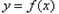 在点
在点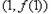 处的切线方程为
处的切线方程为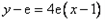 ,即
,即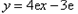 。
。 (2)令
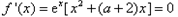 ,解得
,解得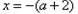 或
或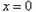 ,
,当
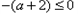 ,即
,即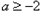 时,在区间
时,在区间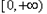 上,
上,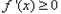 ,
,所以
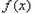 是
是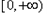 上的增函数,
上的增函数,所以
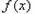 的最小值为
的最小值为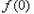 =
=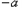 ;
;当
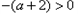 ,即
,即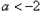 时,
时,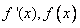 随
随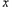 的变化情况如下表
的变化情况如下表
由上表可知函数f(x)的最小值为
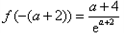 。
。 
练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目