题目内容
如图,已知椭圆C: (a>b>0)的离心率为
(a>b>0)的离心率为 ,左、右焦点分别为F1和F2,椭圆C与x轴的两交点分别为A、B,点P是椭圆上一点(不与点A、B重合),且∠APB=2α,∠F1PF2=2β.
,左、右焦点分别为F1和F2,椭圆C与x轴的两交点分别为A、B,点P是椭圆上一点(不与点A、B重合),且∠APB=2α,∠F1PF2=2β.(Ⅰ)若β=45°,三角形F1PF2的面积为36,求椭圆C的方程;
(Ⅱ)当点P在椭圆C上运动,试证明tanβ•tan2α为定值.

【答案】分析:(Ⅰ)由题意三角形F1PF2为直角三角形,所以 ,即
,即 ,结合三角形F1PF2的面积为36,可求得b2=36,利用椭圆C的离心率为
,结合三角形F1PF2的面积为36,可求得b2=36,利用椭圆C的离心率为 ,可得a2=100,从而可求椭圆C的方程;
,可得a2=100,从而可求椭圆C的方程;
(Ⅱ)不妨设点P(x,y)在第一象限,则在三角形PF1F2中, ,从而可得4c2=4a2-2|PF1||PF2|(1+cos2β),进而有
,从而可得4c2=4a2-2|PF1||PF2|(1+cos2β),进而有 =
= .
.
由 ,可得
,可得 .作PC⊥x轴,垂足为C,故可求得
.作PC⊥x轴,垂足为C,故可求得 ,进而得
,进而得 ,利用离心率
,利用离心率 ,可求tanβ•tan2α是定值.
,可求tanβ•tan2α是定值.
解答: 解:(Ⅰ)∵∠F1PF2=2β=90°
解:(Ⅰ)∵∠F1PF2=2β=90°
∴三角形F1PF2为直角三角形,
∴ ,
,
∴ ,
,
∵三角形F1PF2的面积为36,
∴ ,
,
∴|PF1||PF2|=72
∴(2a)2-2×72=(2c)2,
∴b2=36. …(2分)
∵椭圆C的离心率为 ,则
,则 ,即
,即 ,
,
∴a2=100,
∴椭圆C的方程为 . …(4分)
. …(4分)
(Ⅱ)不妨设点P(x,y)在第一象限,则在三角形PF1F2中, ,
,
∴ ,
,
即4c2=4a2-2|PF1||PF2|(1+cos2β),
∴ .
.
∴ =
= .
.
∵ ,
,
∴b2tanβ=cy,即 . …(6分)
. …(6分)
作PC⊥x轴,垂足为C.
∵ ,
, ,
,
∴ .
.
∵ ,∴
,∴ .
.
∴ . …(8分)
. …(8分)
∴ ,
,
∵离心率 ,
,
∴ .
.
∴tanβ•tan2α是定值,其值为 . …(10分)
. …(10分)
点评:本题以椭圆的性质为载体,考查椭圆的标准方程,考查焦点三角形的面积计算,考查余弦定理的运用,综合性强.
 ,即
,即 ,结合三角形F1PF2的面积为36,可求得b2=36,利用椭圆C的离心率为
,结合三角形F1PF2的面积为36,可求得b2=36,利用椭圆C的离心率为 ,可得a2=100,从而可求椭圆C的方程;
,可得a2=100,从而可求椭圆C的方程;(Ⅱ)不妨设点P(x,y)在第一象限,则在三角形PF1F2中,
 ,从而可得4c2=4a2-2|PF1||PF2|(1+cos2β),进而有
,从而可得4c2=4a2-2|PF1||PF2|(1+cos2β),进而有 =
= .
.由
 ,可得
,可得 .作PC⊥x轴,垂足为C,故可求得
.作PC⊥x轴,垂足为C,故可求得 ,进而得
,进而得 ,利用离心率
,利用离心率 ,可求tanβ•tan2α是定值.
,可求tanβ•tan2α是定值.解答:
 解:(Ⅰ)∵∠F1PF2=2β=90°
解:(Ⅰ)∵∠F1PF2=2β=90°∴三角形F1PF2为直角三角形,
∴
 ,
,∴
 ,
,∵三角形F1PF2的面积为36,
∴
 ,
,∴|PF1||PF2|=72
∴(2a)2-2×72=(2c)2,
∴b2=36. …(2分)
∵椭圆C的离心率为
 ,则
,则 ,即
,即 ,
,∴a2=100,
∴椭圆C的方程为
 . …(4分)
. …(4分)(Ⅱ)不妨设点P(x,y)在第一象限,则在三角形PF1F2中,
 ,
,∴
 ,
,即4c2=4a2-2|PF1||PF2|(1+cos2β),
∴
 .
.∴
 =
= .
.∵
 ,
,∴b2tanβ=cy,即
 . …(6分)
. …(6分)作PC⊥x轴,垂足为C.
∵
 ,
, ,
,∴
 .
.∵
 ,∴
,∴ .
.∴
 . …(8分)
. …(8分)∴
 ,
,∵离心率
 ,
,∴
 .
.∴tanβ•tan2α是定值,其值为
 . …(10分)
. …(10分)点评:本题以椭圆的性质为载体,考查椭圆的标准方程,考查焦点三角形的面积计算,考查余弦定理的运用,综合性强.

练习册系列答案
相关题目
 如图,已知椭圆C:
如图,已知椭圆C: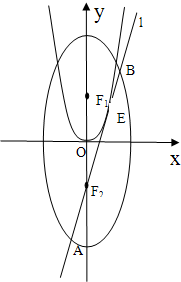 如图,已知椭圆
如图,已知椭圆 如图,已知椭圆C:
如图,已知椭圆C: 如图,已知椭圆
如图,已知椭圆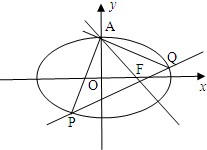 (2012•梅州一模)如图,已知椭圆C:
(2012•梅州一模)如图,已知椭圆C: