题目内容
给出四个命题:
(1)若cosα=cosβ,则α=β;
(2)函数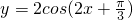 的图象关于直线
的图象关于直线 对称;
对称;
(3)函数y=sin|x|是周期函数,且周期为2π;
(4)函数y=cosx(x∈R)为偶函数.
其中所有正确命题的序号是________.
解:(1)若cosα=cosβ,则α=β,应该为α=2kπ±β,k∈Z,所以(1)不正确;
(2) 时函数
时函数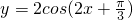 =0,所以函数的图象关于直线
=0,所以函数的图象关于直线 对称,不正确;
对称,不正确;
(3)函数y=sin|x|是周期函数,且周期为2π;应该是:π;不正确;
(4)函数y=cosx(x∈R)为偶函数.是正确的.
故答案为:(4).
分析:通过三角方程的求解判断(1);把 代 入函数是否取得最值,判断(2)是否正确;利用三角函数的周期性判断(3)的正误;利用基本三角函数的性质判断(4)的正误.
代 入函数是否取得最值,判断(2)是否正确;利用三角函数的周期性判断(3)的正误;利用基本三角函数的性质判断(4)的正误.
点评:本题考查三角函数的基本性质,三角方程的解法,对称性,周期性,考查计算能力,基本知识的应用.
(2)
 时函数
时函数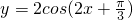 =0,所以函数的图象关于直线
=0,所以函数的图象关于直线 对称,不正确;
对称,不正确;(3)函数y=sin|x|是周期函数,且周期为2π;应该是:π;不正确;
(4)函数y=cosx(x∈R)为偶函数.是正确的.
故答案为:(4).
分析:通过三角方程的求解判断(1);把
 代 入函数是否取得最值,判断(2)是否正确;利用三角函数的周期性判断(3)的正误;利用基本三角函数的性质判断(4)的正误.
代 入函数是否取得最值,判断(2)是否正确;利用三角函数的周期性判断(3)的正误;利用基本三角函数的性质判断(4)的正误.点评:本题考查三角函数的基本性质,三角方程的解法,对称性,周期性,考查计算能力,基本知识的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
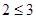 ; (2)如果
; (2)如果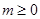 , 则方程
, 则方程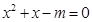 有实根; (3)
有实根; (3)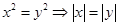 ; (4)“
; (4)“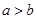 ”是 “
”是 “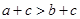 ”的充要条件,其中正确命题的个数有( )个
”的充要条件,其中正确命题的个数有( )个