题目内容
如图,直四棱柱ABCD-A1B1C1D1的高为3,底面是边长为4且∠DAB=60°的菱形,A1C1∩B1D1=O1,E是O1A的中点.(Ⅰ)求二面角O1-BC-D的大小;
(Ⅱ)求点E到平面O1BC的距离.

解法一:(Ⅰ)过AC、BD的交点O作OF⊥BC于F,连接O1F,

∵OO1⊥面AC,∴BC⊥O1F,
∴∠O1FO是二面角O1-BC-D的平面角,
∵OB=2,∠OBF=60°,∴OF=![]() .
.
在Rt△O1OF中,tan∠O1FO=![]() ,
,
∴∠O1FO=60°即二面角O1—BC—D为60°
(Ⅱ)在△O1AC中,OE是△O1AC的中位线,
∴OE∥O1C,∴OE∥面O1BC,
∵BC⊥面O1OF,∴面O1BC⊥面O1OF,交线O1F.
过O作OH⊥O1F于H,则OH是点O到面O1BC的距离,
∴OH=![]() .∴点E到面O1BC的距离等于
.∴点E到面O1BC的距离等于![]() .
.
解法二:(Ⅰ)∵OO1⊥平面AC,
∴OO1⊥OA,OO1⊥OB,又OA⊥OB,
建立如图所示的空间直角坐标系(如图)

∵底面ABCD是边长为4,∠DAB=60°的菱形,
∴OA=2![]() ,OB=2,
,OB=2,
则A(2![]() ,0,0),B(0,2,0),C(-2
,0,0),B(0,2,0),C(-2![]() ,0,0),O1(0,0,3)
,0,0),O1(0,0,3)
设平面O1BC的法向量为n1=(x,y,z),
则n1⊥![]() ,n1⊥
,n1⊥![]() ,
,
∴ ,则z=2,则x=
,则z=2,则x=![]() ,y=3,
,y=3,
∴n1=(![]() ,3,2),而平面AC的法向量n2=(0,0,3)
,3,2),而平面AC的法向量n2=(0,0,3)
∴cos<n1,n2>=![]() ,
,
设O1-BC-D的平面角为α,∴cosα=![]() ;∴α=60°.
;∴α=60°.
故二面角O1-BC-D为60°.
(Ⅱ)设点E到平面O1BC的距离为d,
∵E是O1A的中点,∴![]() =(
=(![]() ,0,
,0,![]() ),
),
则d=

∴点E到面O1BC的距离等于![]()

练习册系列答案
相关题目
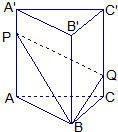 如图:直三棱柱ABC-A′B′C′的体积为V,点P、Q分别在侧棱AA′和CC′上,AP=C′Q,则四棱锥B-APQC的体积为
如图:直三棱柱ABC-A′B′C′的体积为V,点P、Q分别在侧棱AA′和CC′上,AP=C′Q,则四棱锥B-APQC的体积为 如图,直三棱柱ABC-A1B1C1中,AB⊥BC,D为AC的中点,AA1=AB=2.
如图,直三棱柱ABC-A1B1C1中,AB⊥BC,D为AC的中点,AA1=AB=2. 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,∠ABC=45°,其侧面展开图是边长为8的正方形.E、F分别是侧棱AA1、CC1上的动点,AE+CF=8.
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,∠ABC=45°,其侧面展开图是边长为8的正方形.E、F分别是侧棱AA1、CC1上的动点,AE+CF=8. (2012•房山区二模)如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,且∠ABC=60°,E为棱CD的中点.
(2012•房山区二模)如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,且∠ABC=60°,E为棱CD的中点. 如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.
如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.