题目内容
已知抛物线的顶点为椭圆![]()
![]() 的中心.椭圆的离心率是抛物线离心率的一半,且它们的准线互相平行。又抛物线与椭圆交于点
的中心.椭圆的离心率是抛物线离心率的一半,且它们的准线互相平行。又抛物线与椭圆交于点![]() ,求抛物线与椭圆的方程.
,求抛物线与椭圆的方程.
![]() ,
,![]()
解析:
因为椭圆的准线垂直于![]() 轴且它与抛物线的准线互相平行
轴且它与抛物线的准线互相平行
所以抛物线的焦点在![]() 轴上,可设抛物线的方程为
轴上,可设抛物线的方程为![]()
![]() 在抛物线上
在抛物线上
![]()
![]()
![]() 抛物线的方程为
抛物线的方程为![]()
![]() 在椭圆上
在椭圆上 ![]() ①
①
又![]() ②
②
由①②可得![]()
![]() 椭圆的方程是
椭圆的方程是![]()

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
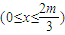 和椭圆弧
和椭圆弧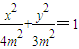

 和椭圆弧
和椭圆弧
